练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知函数f（x）=$\frac{1}{{3}^{x}+1}$，则f（log23）+f（log4$\frac{1}{9}$）=1．

    分析 由于log23+$lo{g}_{4}\frac{1}{9}$=0，f（-x）+f（x）=1，即可得出．

    解答 解：∵log23+$lo{g}_{4}\frac{1}{9}$=log23-log23=0，
    f（-x）+f（x）=$\frac{1}{{3}^{-x}+1}$+$\frac{1}{{3}^{x}+1}$=$\frac{{3}^{x}}{1+{3}^{x}}$+$\frac{1}{{3}^{x}+1}$=1，
    ∴f（log23）+f（log4$\frac{1}{9}$）=1，
    故答案为：1．

    点评 本题考查了指数函数与对数函数的运算性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=ln（1+mx）+$\frac{{x}^{2}}{2}$-mx，其中0＜m≤1．
    （1）当m=1时，求证：-1＜x≤0时，f（x）≤$\frac{{x}^{3}}{3}$；
    （2）试讨论函数y=f（x）的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

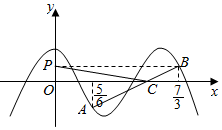    9．如图，已知函数y=sin（$\frac{π}{2}$-πx）的部分图象，点A（$\frac{5}{6}$，m），B（${\frac{7}{3}$，n）为函数图象上的点，线段AB与x轴交于点C，及y轴上点P（0，n），则$\overrightarrow{PC}$•$\overrightarrow{AB}$=（　　）
    A．$\frac{{25-11\sqrt{3}}}{8}$B．$\frac{{25-9\sqrt{3}}}{8}$C．$\frac{{35-11\sqrt{3}}}{8}$D．$\frac{{35-9\sqrt{3}}}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知抛物线y2=8x的准线过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的一个焦点，且双曲线的一条渐近线方程为$\sqrt{3}$x+y=0，则该双曲线的方程为（　　）
    A．$\frac{x^2}{3}$-y2=1B．x2-$\frac{y^2}{3}$=1C．$\frac{x^2}{6}$-$\frac{y^2}{2}$=1D．$\frac{x^2}{2}$-$\frac{y^2}{6}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知等比数列{an}的前n项和是Sn，且S20=21，S30=49，则S10为（　　）
    A．7B．9C．63D．7或63

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．为了解某地参加2015年夏令营的400名学生的身体健康情况，将学生编号为001，002，…，400，采用系统抽样的方法抽取一个容量为40的样本，且抽取到的最小号码为005，已知这400名学生分住在三个营区，从001至155在第一营区，从156到255在第二营区，从256到400在第三营区，则第一，第二，第三营区被抽中的人数分别为（　　）
    A．15，10，15B．16，10，14C．15，11，14D．16，9，15

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

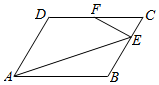    10．在平行四边形ABCD中，AB=4，AD=3，∠DAB=$\frac{π}{3}$，点E，F分别在BC，DC边上，且$\overrightarrow{BE}$=2$\overrightarrow{EC}$，$\overrightarrow{DF}$=$\overrightarrow{FC}$，则$\overrightarrow{AE}$•$\overrightarrow{EF}$=（　　）
    A．-$\frac{8}{3}$B．-3C．-6D．$\frac{10}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．△ABC中，AB=5，AC=2$\sqrt{5}$，BC上的高AH=4，$\overrightarrow{AH}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，则$\frac{x}{y}$=$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知曲线f（x）=（x+a）1nx（a∈R）在点（1，f（1））处的切线与直线x+y+1=0垂直．
    （1）求f（x）的解析式．
    （2）若?x∈[1，+∞），f（x）≤k（x2-1）恒成立，求实数k的取值范围；
    （3）求证：lnn+$\frac{1}{2}$+$\frac{1}{2n}$≤1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$，n∈N•．

    查看答案和解析>>

    同步练习册答案