
 ��ƽ���ı���ABCD�У�AB=4��AD=3����DAB=$\frac{��}{3}$����E��F�ֱ���BC��DC���ϣ���$\overrightarrow{BE}$=2$\overrightarrow{EC}$��$\overrightarrow{DF}$=$\overrightarrow{FC}$����$\overrightarrow{AE}$•$\overrightarrow{EF}$=��������
��ƽ���ı���ABCD�У�AB=4��AD=3����DAB=$\frac{��}{3}$����E��F�ֱ���BC��DC���ϣ���$\overrightarrow{BE}$=2$\overrightarrow{EC}$��$\overrightarrow{DF}$=$\overrightarrow{FC}$����$\overrightarrow{AE}$•$\overrightarrow{EF}$=��������| A�� | -$\frac{8}{3}$ | B�� | -3 | C�� | -6 | D�� | $\frac{10}{3}$ |
���� ����֪��$\overrightarrow{AE}$��$\overrightarrow{EF}$ת��Ϊ����$\overrightarrow{AB}��\overrightarrow{AD}$�Ĵ���ʽ������$\overrightarrow{AE}$•$\overrightarrow{EF}$��չ������������ô𰸣�
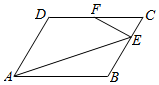
��� �⣺��ͼ��
��AB=4��AD=3����DAB=$\frac{��}{3}$����$\overrightarrow{BE}$=2$\overrightarrow{EC}$��$\overrightarrow{DF}$=$\overrightarrow{FC}$��
��$\overrightarrow{AE}$•$\overrightarrow{EF}$=$��\overrightarrow{AB}+\overrightarrow{BE}��•��\overrightarrow{EC}+\overrightarrow{CF}��$=$��\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}��•��\frac{1}{3}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}��$
=$\frac{2}{9}{\overrightarrow{AD}}^{2}-\frac{1}{2}{\overrightarrow{AB}}^{2}=\frac{2}{9}��9-\frac{1}{2}��16=-6$��
��ѡ��C��
���� ���⿼��ƽ�����������������㣬�����������Ӽ����������η������е��⣮


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| X | 1 | 2 | �� | n | �� |
| P | $\frac{1}{2}$ | $\frac{1}{{2}^{2}}$ | �� | $\frac{1}{{2}^{n}}$ | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com