
分析 (Ⅰ)设公差为d,首项为a1,由a2=5,前4项和为S4=28,得到方程组,解得即可,
(Ⅱ)利用错位相减法即可求出Tn.
解答 解:(Ⅰ)设公差为d,首项为a1,
由a2=5,前4项和为S4=28,得$\left\{\begin{array}{l}{{a}_{2}={a}_{1}+d=5}\\{{S}_{4}=4{a}_{1}+\frac{4(4-1)d}{2}=28}\end{array}\right.$,
解得a1=1,d=4,
∴an=1+4(n-1)=4n-3,
(Ⅱ)bn=2n,Tn=anb1+an-1b2+an-2b3+…+a2bn-1+a1bn,
∴Tn=(4n-3)×2+(4n-7)×22+(4n-11)×23+…+5×2n-1+1×2n,
∴2Tn=(4n-3)×22+(4n-7)×23+(4n-11)×24+…+5×2n+1×2n+1,
∴Tn=-(4n-3)×2+4×22+4×23+4×24+…+4×2n+1×2n+1,
=-8n-2+4(2+22+23+24+…+×2n)+2n+1,
=-8n-2+4$•\frac{2(1-{2}^{n})}{1-2}$+2n+1,
=-8n-10+5•2n+1
点评 本题主要考察等差数列和等比数列的综合问题.解决这类问题的关键在于熟练掌握基础知识,基本方法.并考察计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}$-y2=1 | B. | x2-$\frac{y^2}{3}$=1 | C. | $\frac{x^2}{6}$-$\frac{y^2}{2}$=1 | D. | $\frac{x^2}{2}$-$\frac{y^2}{6}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15,10,15 | B. | 16,10,14 | C. | 15,11,14 | D. | 16,9,15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
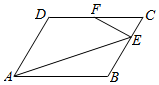 在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=2$\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$•$\overrightarrow{EF}$=( )
在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=2$\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$•$\overrightarrow{EF}$=( )| A. | -$\frac{8}{3}$ | B. | -3 | C. | -6 | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2)(3) | B. | (1)(4) | C. | (1)(2)(4) | D. | (1)(3)(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com