【题目】在直角坐标系
中，曲线
的参数方程为
（
为参数）.以坐标原点
为极点，
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线的极坐标方程和曲线的参数方程；
（2）若曲线
与曲线，在第一象限分别交于
两点，且
，求
的取值范围.
科目：高中数学 来源： 题型：
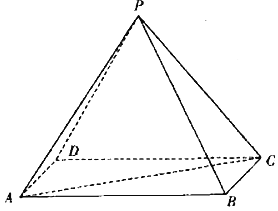
【题目】如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，AB=2AD=2，∠DAB=60°，PA=PC=2，且平面ACP⊥平面ABCD．
（Ⅰ）求证：CB⊥PD；
（Ⅱ）求二面角C-PB-A的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆
．
（1）若椭圆
，判断
与
是否相似？如果相似，求出与的相似比；如果不相似，请说明理由；
（2）写出与椭圆相似且短半轴长为
的椭圆
的方程；若在椭圆上存在两点
、
关于直线
对称，求实数的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】关于
的方程组
的系数矩阵记为
，且该方程组存在非零解，若存在三阶矩阵
，使得
，（0表示零矩阵，即所有元素均为0的矩阵；矩阵
对应的行列式为
），则
（1）
一定为1；
（2）一定为0；
（3）该方程组一定有无穷多解.
其中正确说法的个数是（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度，研究人员在
地各个国企中随机抽取了1000名员工进行调查，并将满意程度以分数的形式统计成如下的频率分布直方图，其中
.
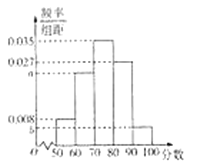
（Ⅰ）估计被调查的员工的满意程度的中位数；（计算结果保留两位小数）
（Ⅱ）若按照分层抽样从
，
中随机抽取8人，再从这8人中随机抽取4人，记分数在的人数为
，求的分布列与数学期望；
（Ⅲ）以频率估计概率，若该研究人员从全国国企员工中随机抽取
人作调查，记成绩在，
的人数为，若
，求的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.
（1）求曲线的极坐标方程和曲线的参数方程；
（2）若曲线与曲线，在第一象限分别交于两点，且，求的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某大城市一家餐饮企业为了了解外卖情况，统计了某个送外卖小哥某天从9:00到21:00这个时间段送的50单外卖.以2小时为一时间段将时间分成六段，各时间段内外卖小哥平均每单的收入情况如下表，各时间段内送外卖的单数的频率分布直方图如下图.
时间区间 |
|
|
|
|
|
|
每单收入（元） | 6 | 5.5 | 6 | 6.4 | 5.5 | 6.5 |
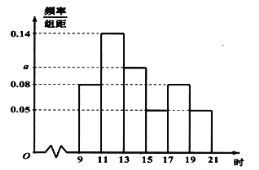
（Ⅰ）求频率分布直方图中
的值，并求这个外卖小哥送这50单获得的收入；
（Ⅱ）在这个外卖小哥送出的50单外卖中男性订了25单，且男性订的外卖中有20单带饮品，女性订的外卖中有10单带饮品，请完成下面的
列联表，并回答是否有
的把握认为“带饮品和男女性别有关”？
带饮品 | 不带饮品 | 总计 | |
男 | |||
女 | |||
总计 |
附：
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】记无穷数列
的前
项中最大值为
，最小值为
，令
．
（1）若
，写出
，
，
，
的值；
（2）设
，若
，求
的值及
时数列
的前项和
；
（3）求证：“数列是等差数列”的充要条件是“数列是等差数列”．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
