
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)证明:当![]() 时,
时,![]() .
.
【答案】(1)![]() 在
在![]() 处取得极小值为
处取得极小值为![]() ,无极大值;(2)详见解析.
,无极大值;(2)详见解析.
【解析】
(1)当a=1时,f(x)=(x﹣1)ex+x2.f′(x)=xex+2x=x(ex+2),令f′(x)=0,解得x.即可得出极值;(2)令h(x)=f(x)﹣ln(ax﹣1)﹣x2﹣x﹣1=(ax﹣1)ex﹣ln(ax﹣1)﹣x﹣1.x![]() .h′(x)=(ax﹣1+a)ex
.h′(x)=(ax﹣1+a)ex![]() 1=(ax﹣1+a)(ex
1=(ax﹣1+a)(ex![]() ).令u(x)=ex
).令u(x)=ex![]() ,利用导数研究其单调性极值即可得出.
,利用导数研究其单调性极值即可得出.
(1)当![]() 时,
时,![]()
![]()
令![]() 得
得![]()
当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增;
单调递增;
所以![]() 在
在![]() 处取得极小值为
处取得极小值为![]() ,无极大值.
,无极大值.
(2)设![]()
![]()
则![]()
![]()
![]()
设![]() ,则
,则![]()
![]() 在区间
在区间![]() 上单调递增
上单调递增
又![]() ,当
,当![]() 时,
时,![]() ,由
,由![]() ,解得
,解得![]() ,
,
当![]() 时,
时, ![]() ,故
,故![]() 有唯一的零点
有唯一的零点![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
且![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]()


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
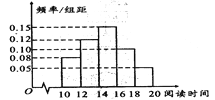
【题目】某教师将寒假期间该校所有学生阅读小说的时间统计如下图所示,并统计了部分学生阅读小说的类型,得到的数据如下表所示:
男生 | 女生 | |
阅读武侠小说 | 80 | 30 |
阅读都市小说 | 20 | 70 |
(1)是否有99.9%的把握认为“性别”与“阅读小说的类型”有关?
(2)求学生阅读小说时间的众数和平均数(同一组数据用该组区间的中点值作代表);
(3)若按照分层抽样的方法从阅读时间在![]() 、
、![]() 的学生中随机抽取6人,再从这6人中随机挑选2人介绍选取小说类型的缘由,求所挑选的2人阅读时间都在
的学生中随机抽取6人,再从这6人中随机挑选2人介绍选取小说类型的缘由,求所挑选的2人阅读时间都在![]() 的概率.
的概率.
附:![]() ,
,![]() .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
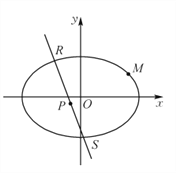
【题目】如图,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() .
.
(l)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() 且直线
且直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列判断正确的是()
对称,则下列判断正确的是()
A. 函数![]() 在
在![]() 上单调递增
上单调递增
B. 函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
C. 当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
D. 要得到函数![]() 的图像,只需要
的图像,只需要![]() 将的图像向右平移
将的图像向右平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若数列![]() 、
、![]() 的极限都存在,且
的极限都存在,且![]() ,则数列
,则数列![]() 的极限存在
的极限存在
B.若数列![]() 、
、![]() 的极限都不存在,则数列
的极限都不存在,则数列![]() 的极限也不存在
的极限也不存在
C.若数列![]() 、
、![]() 的极限都存在,则数列
的极限都存在,则数列![]() 、
、![]() 的极限也存在
的极限也存在
D.数![]() ,若数列
,若数列![]() 的极限存在,则数列
的极限存在,则数列![]() 的极限也存在
的极限也存在
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若曲线![]() 与曲线
与曲线![]() ,
,![]() 在第一象限分别交于
在第一象限分别交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若曲线![]() 与曲线
与曲线![]() ,
,![]() 在第一象限分别交于
在第一象限分别交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com