分析:(1)根据两角和与差的正弦函数公式分别化简分子与分母,然后利用诱导公式cos80°=cos(90°-10°)=sin10°
及cot15°=
=
,利用特殊角的三角函数值求出即可.
(2)因为cosθ≠0,所以化简sinθ+2cosθ=0得:tanθ=-2,然后把原式的分子利用二倍角的正弦、余弦函数公式化简,分母利用同角三角函数间的基本关系把1=sin
2θ+cos
2θ;然后对分子分母都除以cos
2θ进行化简,然后把tanθ代入求出值即可.
解答:解:(1)原式=
| sin(80°-15°)+sin15°sin10° |
| sin(15°+10°)-cos15°cos80° |
=
| sin80°cos15°-cos80°sin15°+sin15°sin10° |
| sin15°cos10°+cos15°sin10°-cos15°cos80° |
=
| sin80°cos15°-sin10°sin15°+sin10°sin15° |
| sin15°cos10°+cos15°sin10°-cos15°sin10° |
=
=
=
=cot15°
=
=
=
| 1+tan45°tan30° |
| tan45°-tan30° |
=
=2+
;
(2)由sinθ+2cosθ=0,得sinθ=-2cosθ,又cosθ≠0,则tanθ=-2,
所以
=| cos2θ-sin2θ-2sinθcosθ |
| sin2θ+2cos2θ |
=
==.
点评:考查学生灵活运用两角和与差的正弦、余弦函数公式化简求值,会进行弦切互化,灵活运用同角三角函数间的基本关系化简求值,会利用特殊角的三角函数值进行化简求值.以及会利用二倍角的正弦、余弦函数公式进行化简求值.



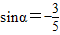 ,且α为第三象限角,求cosα,cos2α的值
,且α为第三象限角,求cosα,cos2α的值