Question

5．在平面几何中有正确的结论，已知一个正三角形的内切圆面积为S₁，外接圆面积为S₂，则$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{4}$，类比上述结论推理，在空间中，已知一个正四面体的内切球体积为V₁，外接球体积为V₂，则$\frac{{V}_{1}}{{V}_{2}}$=（　　）

• A． $\frac{1}{3}$
• B． $\frac{1}{8}$
• C． $\frac{1}{16}$
• D． $\frac{1}{27}$

Answer 1

分析 设正四面体棱长为1，求出棱锥的高，利用等体积法求出内切球的半径r，利用勾股定理求出外接球的半径R，得出两球的体积比．

解答 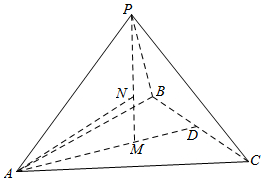解：设正四面体的棱长为1，取BC的中点D，连结AD，作正四面体的高PM．
则AD=$\frac{\sqrt{3}}{2}$，AM=$\frac{2}{3}AD$=$\frac{\sqrt{3}}{3}$，∴PM=$\sqrt{P{A}^{2}-A{M}^{2}}$=$\frac{\sqrt{6}}{3}$．
∴V_P-ABC=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{1}^{2}×\frac{\sqrt{6}}{3}$=$\frac{\sqrt{2}}{12}$．
设内切球的半径为r，内切球球心为O，则V_P-ABC=4V_O-ABC=4×$\frac{1}{3}×\frac{\sqrt{3}}{4}×{1}^{2}×r$，
解得r=$\frac{\sqrt{6}}{12}$．
设外接球的半径为R，外接球球心为N，则MN=|PM-R|或|R-PM|，AN=R，
在Rt△AMN中，由勾股定理得AM²+MN²=AN²，
∴$\frac{1}{3}$+（$\frac{\sqrt{6}}{3}$-R）²=R²，解得R=$\frac{\sqrt{6}}{4}$．
∴$\frac{r}{R}=\frac{1}{3}$．
∴$\frac{{V}_{1}}{{V}_{2}}$=$\frac{{r}^{3}}{{R}^{3}}$=$\frac{1}{27}$．
故选D．

点评 本题考查了棱锥与外接球，内切球的关系，属于中档题．