
【题目】设![]() ,
,![]()
(1)求![]() 在区间
在区间![]() 上的值域;
上的值域;
(2)求![]() 在区间
在区间![]() 上的值域:
上的值域:
(3)已知![]() ,若对于任意
,若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见详解 (3)
(2)见详解 (3)![]()
【解析】
(1) 根据题意,判断出![]() 在
在![]() 上的单调性,即可求出
上的单调性,即可求出![]() 在区间
在区间![]() 上的值域;
上的值域;
(2) 根据题意,先求出![]() 的对称轴,再根据区间
的对称轴,再根据区间![]() 与对称轴的位置关系进行分类讨论,即可求出
与对称轴的位置关系进行分类讨论,即可求出![]() 在区间
在区间![]() 上的值域;
上的值域;
(3) 根据题意,只需满足![]() 在区间
在区间![]() 上的值域是
上的值域是![]() 在区间
在区间![]() 上的值域的子集,根据集合之间的包含关系即可求得
上的值域的子集,根据集合之间的包含关系即可求得![]() 的取值范围。
的取值范围。
(1) 根据题意,可得![]()
易知![]() 在
在![]() 上是单调递增的,
上是单调递增的,
![]()
![]()
![]() 在区间
在区间![]() 上的值域为
上的值域为![]() .
.
(2)由题意得,![]() 的对称轴为
的对称轴为![]() ,则
,则
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 上先减后增,
上先减后增,
![]()
若![]() ,则
,则 ![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
若![]() ,则
,则 ![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
若![]() ,则
,则 ![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
(3) 根据(1)(2)可知,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,当
,当![]() 时,
时,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;若对于任意
;若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,只需满足
成立,只需满足![]() 在区间
在区间![]() 上的值域是
上的值域是![]() 在区间
在区间![]() 上的值域的子集,即
上的值域的子集,即

解得![]()


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,C为直线y=5上的动点,以C为圆心的圆C截y轴所得的弦长恒为6,过原点O作圆C的一条切线,切点为P,则点P到直线3x+4y﹣25=0的距离的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.
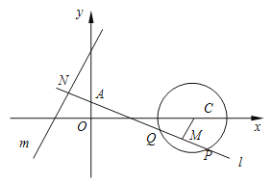
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() . 探索
. 探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商店出售茶壶和茶杯,茶壶定价每个20元,茶杯每个5元,该商店推出两种优惠办法:(1)买一个茶壶赠一个茶杯;(2)按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款y(元),分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三有500名学生,在一次考试的英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
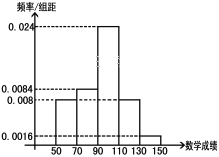
(Ⅰ)如果成绩大于135的为特别优秀,则本次考试英语、数学特别优秀的大约各多少人?
(Ⅱ)试问本次考试英语和数学的成绩哪个较高,并说明理由.
(Ⅲ)如果英语和数学两科都特别优秀的共有6人,从(Ⅰ)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望。
的分布列和数学期望。
参考公式及数据:
若![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抽样得到某次考试中高二年级某班![]() 名学生的数学成绩和物理成绩如下表:
名学生的数学成绩和物理成绩如下表:
学生编号 |
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
物里成绩 |
|
|
|
|
|
|
(1)在图中画出表中数据的散点图;
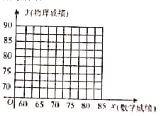
(2)建立![]() 关于
关于![]() 的回归方程:(系数保留到小数点后两位).
的回归方程:(系数保留到小数点后两位).
(3)如果某学生的数学成绩为![]() 分,预测他本次的物理成绩(成绩取整数).
分,预测他本次的物理成绩(成绩取整数).
参考公式:回归方程为![]() ,其中
,其中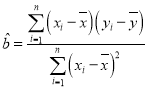 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国青年报》2015年5月14日报道:“伴随着网络技术的蓬勃发展,国内电子商务获得了爆炸式的增长,2014年网上零售额达到了27898亿元,占社会消费品零售总额的10%,也就是说,人们日常消费中10%是通过网购,而且还以年30%,40%的速度增长."假设2014-2020年网上零售额每年的增长率均为35%,试算出2015-2020年每年的网上零售额(精确到1亿元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在促销期间规定:商场内所有商品按标价的![]() 出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围 |
|
|
|
| … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为:![]() 元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,顾客购买标价为多少元的商品,可得到不小于
(元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com