
���� ����ֱ��l�IJ���������ȥ�����������ֱ��l����ͨ���̣�������C�ļ����귽�����������C��ֱ�����귽�̣�������ֱ��l��Բ���У��ɴ������a��ֵ��
������A����1���ȣ���B����2��$��+\frac{��}{3}$������|OA|+|OB|=��1+��2=2cos��+2cos��$��+\frac{��}{3}$��=3cos��-$\sqrt{3}sin��$=2$\sqrt{3}$cos��$��+\frac{��}{6}$�����ɴ������|OA|+|OB|�����ֵ��
��� �⣺����ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-\frac{\sqrt{3}}{2}t}\\{y=\sqrt{3}+\frac{1}{2}t}\end{array}\right.$��tΪ��������
��ֱ��l����ͨ������x+$\sqrt{3}y$-3=0��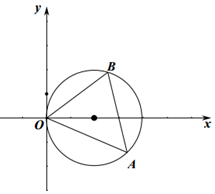
������C�ļ����귽��Ϊ��=2acos�ȣ�a��0����
������C��ֱ�����귽���ǣ�x-a��2+y2=a2��
������ֱ��l��Բ���У���d=$\frac{|a-3|}{2}$=a��
���a=-3����a=1��
��a��0����a=1��
������ͼ��������A����1���ȣ���B����2��$��+\frac{��}{3}$����
���1=2cos�ȣ�${��}_{2}=2cos����+\frac{��}{3}��$��
|OA|+|OB|=��1+��2=2cos��+2cos��$��+\frac{��}{3}$��=3cos��-$\sqrt{3}sin��$=2$\sqrt{3}$cos��$��+\frac{��}{6}$����
���+$\frac{��}{6}$=2k�У���$��=2k��-\frac{��}{6}$��k��Zʱ��|OA|+|OB|���ֵ��2$\sqrt{3}$��
���� ���⿼��ʵ��ֵ�����������߶κ͵�������������̡�ֱ�����귽�̡������귽�̻�����ʽ��Ӧ�ã������������������ת������˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\sqrt{2}$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-2016�� | B�� | ��-2018��-2016�� | ||
| C�� | ��-2018��+�ޣ� | D�� | ��-�ޣ�-2018���ȣ�-2016��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{9}$ | C�� | 3 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com