
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.

(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
【答案】(1)频率为![]() ,全班人数为
,全班人数为![]() ;(2)频数为
;(2)频数为![]() ,矩形的高为
,矩形的高为![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)分数在![]() 的频率为第一组矩形的面积,全班人数为该组的频数与频率的比值;(2)用全班人数送去其余组的人数为
的频率为第一组矩形的面积,全班人数为该组的频数与频率的比值;(2)用全班人数送去其余组的人数为![]() 之间的频数,用该组的频率与组距的组距的比值为矩形的高;(3)首先用列举法列举出所有的基本事件,然后找出符合题意的基本事件个数,从而利用古典概型概率公式计算即可.
之间的频数,用该组的频率与组距的组距的比值为矩形的高;(3)首先用列举法列举出所有的基本事件,然后找出符合题意的基本事件个数,从而利用古典概型概率公式计算即可.
试题解析:(1)分数在![]() 的频率为
的频率为![]() ,
,
由茎叶图知:分数在![]() 之间的频数为2,所以全班人数为
之间的频数为2,所以全班人数为![]() .
.
(2)分数在![]() 之间的频数为
之间的频数为![]() ;
;
频率分布直方图中![]() 间的矩形的高为
间的矩形的高为![]() .
.
(3)将![]() 之间的3个分数编号为
之间的3个分数编号为![]() ,
,![]() 之间的2个分数编号为
之间的2个分数编号为![]() ,
,
在![]() 之间的试卷中任取两份的基本事件为:
之间的试卷中任取两份的基本事件为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10个,
共10个,
其中,至少有一个在![]() 之间的基本事件有7个,
之间的基本事件有7个,
故至少有一份分数在![]() 之间的概率是
之间的概率是![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】为了了解某省各景点在大众中的熟知度,随机对15~65岁的人群抽样了![]() 人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组 | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在育民中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.

(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数是多少;
(3)这两个班参赛学生的成绩的中位数应落在第几小组内.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在原点
的焦点在原点![]() ,左焦点
,左焦点![]() ,左顶点
,左顶点![]() ,上顶点
,上顶点![]() ,
,![]() 的周长为
的周长为![]() ,
,![]() 的面积为
的面积为![]() .
.
(I)求椭圆![]() 的标准方程;
的标准方程;
(II)是否存在与椭圆![]() 交于
交于![]() 两点的直线
两点的直线![]() 使得
使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富高学生的课外生活,某校要组建数学计算机航空模型3个兴趣小组,小明要选报其中的2个,则包含的样本点共有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.
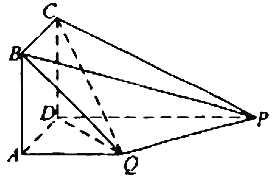
(I)证明:平面PQC⊥平面DCQ
(II)求二面角Q-BP-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com