
【题目】已知函数![]()
![]() ,
,
(1)若曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,求
,求![]() 的值;
的值;
(2)讨论函数![]() 的单调性;
的单调性;
(3)设函数![]() ,若至少存在一个
,若至少存在一个![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范.
的取值范.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,增区间为
时,增区间为![]() ;当
;当![]() 时,增区间为
时,增区间为![]() ,
,![]() ,减区间为
,减区间为![]() ;当
;当![]() 时,增区间为
时,增区间为![]() ,
,![]() ,减区间为
,减区间为![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)首先求得![]() 的定义域及导函数,然后利用导数的几何意义求解即可;(2)分
的定义域及导函数,然后利用导数的几何意义求解即可;(2)分![]() 、
、![]() 、
、![]() 讨论
讨论![]() 的导函数与0的关系,由此求得函数的单调区间;(3)首先根据条件将问题转化为
的导函数与0的关系,由此求得函数的单调区间;(3)首先根据条件将问题转化为 有解,然后令
有解,然后令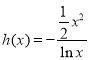 ,从而通过求导得到函数
,从而通过求导得到函数![]() 的单调性,并求得其最小值,进而求得实数
的单调性,并求得其最小值,进而求得实数![]() 的取值范.
的取值范.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
解得![]() ,∴
,∴![]() .
.
(2)![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]()
当![]() 时,由
时,由![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]()
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() .
.
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,![]()
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() .
.
综上所述:当![]() 时,
时, ![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]() ,
,
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]()
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]() .
.
(3)若至少存在一个![]() ,使得
,使得![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴ 有解,令
有解,令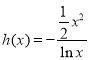 ,
,
∴![]()
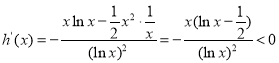 ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,![]()
∴![]() 得,
得,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 为实数且
为实数且![]() .
.
(1)设函数![]() .当
.当![]() 时,
时,![]() 在其定义域内为单调增函数,求
在其定义域内为单调增函数,求![]() 的取值范围;
的取值范围;
(2)设函数![]() .当
.当![]() 时,在区间
时,在区间![]() (其中
(其中![]() 为自然对数的底数)上是否存在实数
为自然对数的底数)上是否存在实数![]() ,使得
,使得![]() 成立,若存在,求实数
成立,若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个家庭有两个小孩,把第一个孩子的性别写在前边,第二个孩子的性别写在后边,则所有的样本点有( )
A.(男,女),(男,男),(女,女)
B.(男,女),(女,男)
C.(男,男),(男,女),(女,男),(女,女)
D.(男,男),(女,女)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.

(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列判断:①一条直线和一点确定一个平面;②两条直线确定一个平面;③三角形和梯形一定是平面图形;④三条互相平行的直线一定共面其中正确的是_______.(写出所有正确判断的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的骰子先后抛掷2次,观察其向上的点数,分别记为![]() .
.
(1)若记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)若记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年五一节”期间,高速公路车辆“较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题:
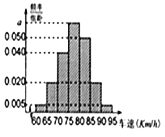
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)若该路段的车速达到或超过90km/h即视为超速行驶,求超速行驶的概率
(3)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com