
【题目】已知函数![]() .
.
(1) 试说明函数![]() 的图象是由函数
的图象是由函数![]() 的图象经过怎样的变换得到的;
的图象经过怎样的变换得到的;
(2)若函数![]() ,试判断函数
,试判断函数![]() 的奇偶性,并用反证法证明函数
的奇偶性,并用反证法证明函数![]() 的最小正周期是
的最小正周期是![]() ;
;
(3)求函数![]() 的单调区间和值域.
的单调区间和值域.
【答案】(1)见解析;(2)偶函数,周期的证明见解析;(3)值域是![]() ,增区间为
,增区间为![]() ,减区间为
,减区间为![]() .
.
【解析】
(1)先由二倍角公式和两角差的正弦公式化函数为一个角的一个三角函数形式,然后根据三角函数图象变换的规律求解;
(2)求出![]() 的表达式,由奇偶性定义判断奇偶性,用反证法证明周期性;
的表达式,由奇偶性定义判断奇偶性,用反证法证明周期性;
(3)根据(2)中得出的性质,在一个周期内求出函数的值域,即得函数在定义域内值域,求出一个周期内单调区间,根据函数的周期性可得所有单调区间(但要注意区间的连续性).
(1)由题意![]() ,
,
把![]() 图象向右平移
图象向右平移![]() 个单位得
个单位得![]() 的图象,再把所得图象上所有点的纵坐标不变,横坐标变为原来的
的图象,再把所得图象上所有点的纵坐标不变,横坐标变为原来的![]() ,得
,得![]() 的图象,最后将所得图象上所有点的纵坐标变为原来的2倍,横坐标不变,得
的图象,最后将所得图象上所有点的纵坐标变为原来的2倍,横坐标不变,得![]() 的图象.
的图象.
(2)![]()
![]() ,
,
![]() ,∴
,∴![]() 是偶函数,
是偶函数,
![]()
![]()
![]() ,
,![]() 是
是![]() 的一个周期,下面用反证法证明
的一个周期,下面用反证法证明![]() 是最小正周期,
是最小正周期,
假设存在![]() 是
是![]() 的最小正周期,即
的最小正周期,即![]() 恒成立,
恒成立,![]() ,
,
则![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,∴
,∴![]() ,即
,即![]() 这与
这与![]() 矛盾,∴假设错误,
矛盾,∴假设错误,
∴![]() 是
是![]() 的最小正周期.
的最小正周期.
(3)由(2),当![]() 时,
时,![]() ,
,
由![]() 得
得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
此时当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
∵![]() 的最小正周期是
的最小正周期是![]() ,∴
,∴![]() 时,函数
时,函数![]() 的值域是
的值域是![]() .
.
增区间为![]() ,减区间为
,减区间为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价![]() (元)与销量
(元)与销量![]() (万件)之间的函数关系如图所示,又知供货价格与销量成反比,比例系数为20.(注:每件产品利润=售价-供货价格)
(万件)之间的函数关系如图所示,又知供货价格与销量成反比,比例系数为20.(注:每件产品利润=售价-供货价格)

(Ⅰ)求售价15元时的销量及此时的供货价格;
(Ⅱ)当销售价格为多少时总利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 的图象关于直线
的图象关于直线![]() 对称,则正确的选项是( )
对称,则正确的选项是( )
①.函数![]() 为奇函数
为奇函数
②.函数![]() 在
在![]() 上单调递增
上单调递增
③.若![]() ,则
,则![]() 的最小值为
的最小值为![]()
④.函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象
的图象
A.①③B.①④C.①②③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
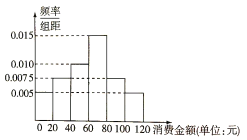
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,以直角坐标系的原点为极点,以
两点,以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2) 已知点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查,得到了如下的统计结果:

(1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(2)完成联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”.

附:![]() ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象上有一点列
的图象上有一点列![]() ,点
,点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() (
(![]() 且
且![]() ),
),![]() .
.
(1)求证:![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设四边形![]() 的面积是
的面积是![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4,坐标系与参数方程】
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为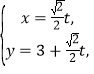 (t为参数),在以O为极点,
(t为参数),在以O为极点,![]() 轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(Ⅱ)若直线![]() 与
与![]() 轴的交点为P,直线
轴的交点为P,直线![]() 与曲线C的交点为A,B,求
与曲线C的交点为A,B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com