
【题目】设函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,求证:函数
,求证:函数![]() 的极大值小于1.
的极大值小于1.
【答案】(1)见解析;(2)![]() (3)见证明
(3)见证明
【解析】
(1)先对函数求导,分别讨论![]() 和
和![]() ,即可得出结果;
,即可得出结果;
(2)先将函数![]() 在
在![]() 时恒成立,转化为
时恒成立,转化为![]() 在
在![]() 上恒成立,再设
上恒成立,再设![]() ,
,![]() ,利用导数方法求出
,利用导数方法求出![]() 的最大值,即可得出结果;
的最大值,即可得出结果;
(3)先由题意得到![]() ,对
,对![]() 求导,利用导数的方法研究其单调性,即可求出其极大值,得出结论.
求导,利用导数的方法研究其单调性,即可求出其极大值,得出结论.
解:(1)由于![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ;
;
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增.
上单调递增.
(2)若![]() 在
在![]() 上恒成立,
上恒成立,
只需![]() ,
,![]() .
.
令![]() ,
,![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,所以
,所以
![]() ,
,![]() 随
随![]() 的变化情况如下:
的变化情况如下:
|
| 1 |
|
| + | 0 | - |
|
| 极大值 |
|
所以![]() ,所以
,所以![]() .
.
(3)由题知![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
则函数![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,
,
所以存在唯一的![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ,
,
其中![]() ,所以函数
,所以函数![]() 有极大值.
有极大值.
函数![]() 的极大值是
的极大值是![]() ,由
,由![]() ,得
,得![]() ,
,
所以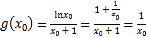 ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 的极大值小于1.
的极大值小于1.


科目:高中数学 来源: 题型:
【题目】某校![]() 位同学的数学与英语成绩如下表所示:
位同学的数学与英语成绩如下表所示:
学号 |
|
|
|
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
|
|
|
英语成绩 |
|
|
|
|
|
|
|
|
|
|
学号 |
|
|
|
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
|
|
|
英语成绩 |
|
|
|
|
|
|
|
|
|
|
将这![]() 位同学的两科成绩绘制成散点图如下:
位同学的两科成绩绘制成散点图如下:
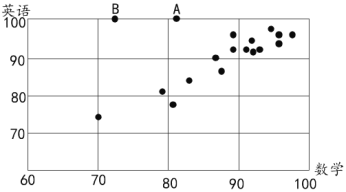
(1)根据该校以往的经验,数学成绩![]() 与英语成绩
与英语成绩![]() 线性相关.已知这
线性相关.已知这![]() 名学生的数学平均成绩为
名学生的数学平均成绩为![]() ,英语平均成绩为
,英语平均成绩为![]() .考试结束后学校经过调查发现学号为
.考试结束后学校经过调查发现学号为![]() 的
的![]() 同学与学号为
同学与学号为![]() 的
的![]() 同学(分别对应散点图中的
同学(分别对应散点图中的![]() 、
、![]() )在英语考试中作弊,故将两位同学的两科成绩取消,取消两位作弊同学的两科成绩后,求其余同学的数学成绩与英语成绩的平均数;
)在英语考试中作弊,故将两位同学的两科成绩取消,取消两位作弊同学的两科成绩后,求其余同学的数学成绩与英语成绩的平均数;
(2)取消两位作弊同学的两科成绩后,求数学成绩![]() 与英语成绩
与英语成绩![]() 的线性回归方程
的线性回归方程![]() ,并据此估计本次英语考试学号为
,并据此估计本次英语考试学号为![]() 的同学如果没有作弊的英语成绩(结果保留整数).
的同学如果没有作弊的英语成绩(结果保留整数).
附:![]() 位同学的两科成绩的参考数据:
位同学的两科成绩的参考数据:![]() ,
,![]() .
.
参考公式: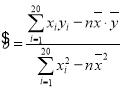 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象中相邻两条对称轴之间的距离为
的图象中相邻两条对称轴之间的距离为![]() ,且直线
,且直线![]() 是其图象的一条对称轴.
是其图象的一条对称轴.

(1)求![]() ,
,![]() 的值;
的值;
(2)在图中画出函数![]() 在区间
在区间![]() 上的图象;
上的图象;
(3)将函数![]() 的图象上各点的横坐标缩短为原来的
的图象上各点的横坐标缩短为原来的![]() (纵坐标不变),再把得到的图象向左平移
(纵坐标不变),再把得到的图象向左平移![]() 个单位,得到
个单位,得到![]() 的图象,求
的图象,求![]() 单调减区间.
单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1) 试说明函数![]() 的图象是由函数
的图象是由函数![]() 的图象经过怎样的变换得到的;
的图象经过怎样的变换得到的;
(2)若函数![]() ,试判断函数
,试判断函数![]() 的奇偶性,并用反证法证明函数
的奇偶性,并用反证法证明函数![]() 的最小正周期是
的最小正周期是![]() ;
;
(3)求函数![]() 的单调区间和值域.
的单调区间和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=![]() ,(m∈R,i是虚数单位).
,(m∈R,i是虚数单位).
(1)若z是纯虚数,求m的值;
(2)设![]() 是z的共轭复数,复数
是z的共轭复数,复数![]() +2z在复平面上对应的点在第一象限,求m的取值范围.
+2z在复平面上对应的点在第一象限,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.
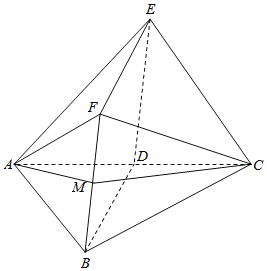
![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是边长为2的正方形,SA=SB=SC=SD![]() ,点E,M,N分别是BC,CD,SC的中点,点P是MN上的一点.
,点E,M,N分别是BC,CD,SC的中点,点P是MN上的一点.

(1)证明:EP∥平面SBD;
(2)求四棱锥S﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)在第(2)问的条件下,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是演绎推理的个数是( )
①两条直线平行,同旁内角互补。如果∠A与∠B是两条平行直线的同旁内角,那么∠A+∠B=180°;
②猜想数列1,3,5,7,9,11,…的通项公式为![]() ;
;
③由正三角形的性质得出正四面体的性质;
④半径为![]() 的圆的面积
的圆的面积![]() ,则单位圆的面积
,则单位圆的面积![]() .
.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com