
【题目】已知![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间和最小值.
的单调区间和最小值.
(2)若![]() 有两个极值求实数
有两个极值求实数![]() 的取值范围。
的取值范围。
(3)若![]() ,且
,且![]() ,比较
,比较![]() 与
与![]() 的大小,并说明理由。
的大小,并说明理由。
【答案】(1)![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() .
.
(2)![]() .
.
(3)![]() ;理由见解析.
;理由见解析.
【解析】分析:(1)对函数求导,利用导数的正负,可得函数的单调区间,从而求得函数的最小值,得到结果;
(2)根据函数有两个极值点,得到其导数等于零有两个不等的正根,且在根的两侧导数的符号是相反的,分类讨论求得结果;
(3)利用导数研究其大小,借助于基本不等式求得结果.
详解:(1)∵![]() ∴
∴![]() ,
,![]()
∴![]() ,令
,令![]() ,解得:
,解得:![]() ,列表得:
,列表得:
|
|
|
|
|
| 0 |
|
| 单调减 | 极小值 | 单调增 |
∴![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
(2)∵![]() 有两个极值点
有两个极值点
∴![]() 在
在![]() 上有两个不同的零点,且零点左右的
上有两个不同的零点,且零点左右的![]() 的符号的相反.
的符号的相反.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上单调增,
上单调增,![]() 在
在![]() 上最多有一个零点,不合题意;
上最多有一个零点,不合题意;
当![]() 时,由
时,由![]() ,解得:
,解得:![]()
∴![]() 时,
时,![]() ,
,![]() 时,
时,![]()
∴![]() 在
在![]() 上单调增,则
上单调增,则![]() 上单调减,
上单调减,![]()
若![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上最多有一个零点,不合题意;若
上最多有一个零点,不合题意;若![]() ,
,![]() ,又
,又![]() ,
,
![]()
(取其他小于0的函数值也可)
设![]() ,
,![]() ,则
,则![]() 在
在![]() 上恒成立
上恒成立
∴![]() 在
在![]() 上单调减 ∴
上单调减 ∴![]() ,则
,则![]() 时,
时,![]()
∵![]() ∴
∴![]() ∴
∴![]()
∴![]() 在
在![]() 、
、![]() 上各有一个零点,且零点两侧的函数符号相反
上各有一个零点,且零点两侧的函数符号相反
∴ ![]()
(3)结论:![]() .下面证明:
.下面证明:
由(1)知:![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增
上单调增
∵![]() ∴
∴![]() ,即
,即![]()
∴![]() ,同理
,同理![]()
∴![]()
∵![]() ,当且仅当
,当且仅当![]() 时取等号,且
时取等号,且![]()
∴![]() ,则
,则![]()
∴![]() ∴
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】设点M(x1 , f(x1))和点N(x2 , g(x2))分别是函数f(x)=ex﹣ ![]() x2和g(x)=x﹣1图象上的点,且x1≥0,x2>0,若直线MN∥x轴,则M,N两点间的距离的最小值为( )
x2和g(x)=x﹣1图象上的点,且x1≥0,x2>0,若直线MN∥x轴,则M,N两点间的距离的最小值为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2+ax+a). (I)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若关于x的不等式f(x)≤ea在[a,+∞)上有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+aln(x+1)(a为常数)
(Ⅰ)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;
(Ⅱ)若函数y=f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)如表所示是某市最近5年个人年平均收入表节选.求y关于x的回归直线方程,并估计第6年该市的个人年平均收入(保留三位有效数字).
年份x | 1 | 2 | 3 | 4 | 5 |
收入y(千元) | 21 | 24 | 27 | 29 | 31 |
其中![]() ,
,![]() ,
,![]() 附1:
附1:![]() =
= ![]() ,
,![]() =
=![]() ﹣
﹣![]()
![]()
(Ⅱ)下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表:
受培时间一年以上 | 受培时间不足一年 | 总计 | |
收入不低于平均值 | 60 | 20 | |
收入低于平均值 | 10 | 20 | |
总计 | 100 |
完成上表,并回答:能否在犯错概率不超过0.05的前提下认为“收入与接受培训时间有关系”.
附2:
P(K2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
附3:
K2=![]() .(n=a+b+c+d)
.(n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C对应的边分别为a、b、c,已知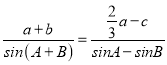 .
.
(1)求cosB的值;
(2)若b=8,cos2A﹣3cos(B+C)=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增大,下表是该地一农业银行连续五年的储蓄存款(年底余额),如下表:

为了研究方便,工作人员将上表的数据进行了处理,![]() ,得到下表:
,得到下表:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)用所求回归方程预测,到2020年底,该地储蓄存款额大约可达多少?
(附:线性回归方程:![]() ,
,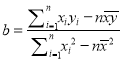 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 过点
过点 ![]() ,左右焦点为F1(﹣c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.
,左右焦点为F1(﹣c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.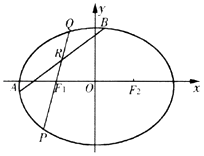
(I)求椭圆C方程;
(II)圆D: ![]() 与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆D的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆D的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com