
 如图所示的几何体中,△ABC为正三角形,AE和CD都垂直于平面ABC,且AE=AB=2,CD=1,F为BE的中点.
如图所示的几何体中,△ABC为正三角形,AE和CD都垂直于平面ABC,且AE=AB=2,CD=1,F为BE的中点.分析 (1)取AB的中点G,证明FG平行且等于CD,可得四边形FMCD为平行四边形,进而得到DF∥CG,从而证明DF∥平面ABC.
(2)取AB中点G,由(1)可知四边形CDFG为平行四边形,可得CG∥DF.根据题意可得:平面ABE⊥平面ABC,可得CG⊥平面ABE,进而得到DF⊥平面ABE,即可证明面面垂直.
解答  (1)证明:取AB中点G,连线FG、CG,F为BE中点,
(1)证明:取AB中点G,连线FG、CG,F为BE中点,
∴GF∥AE,GF=$\frac{1}{2}$AE,又AE⊥平面ABC,CD⊥平面ABC,且CD=$\frac{1}{2}$AE,
∴GF∥CD,GF=CD,
∴四边形CDFG为平行四边形
∴DF∥CG,又DF?平面ABC,CG?平面ABC
∴DF∥平面ABC.
(2)证明:取AB中点G,由(1)可知四边形CDFG为平行四边形,
∴CG∥DF又AE⊥平面ABC,AE?平面ABE
∴平面ABE⊥平面ABC,交线为AB.
又△ABC为正三角形,G为AB中点
∴CG⊥AB,
∴CG⊥平面ABE又CG∥DF,
∴DF⊥平面ABE,
又DF?平面DBE,
∴平面DBE⊥平面ABE.
点评 本题考查证明线面平行以及面面垂直的判定定理,要求熟练掌握相应的判定定理,考查学生的推理能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{2}π}{3}$ | B. | $\frac{8\sqrt{2}π}{3}$ | C. | $\frac{32π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
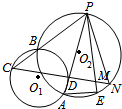 如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.
如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一般齿轮传动装置中有一个主动轮O2和一个从动轮O1,用皮带连接(假设皮带与轮子之间不发生滑动),直线O1O2是一条水平直线,主动轮O2的半径是R,从动轮O1的半径是r,且R=2r,主动轮每分钟逆时针转30圈.开始转动时,从动轮、主动轮上分别标有A1,A2两个点(如图所示),经过t秒A1,A2两个点运动到新位置B1,B2,设B1,B2到水平线O1O2的垂直高度(当A1,A2运动到水平线O1O2下方时,高度是负值)分别是h1,h2.
一般齿轮传动装置中有一个主动轮O2和一个从动轮O1,用皮带连接(假设皮带与轮子之间不发生滑动),直线O1O2是一条水平直线,主动轮O2的半径是R,从动轮O1的半径是r,且R=2r,主动轮每分钟逆时针转30圈.开始转动时,从动轮、主动轮上分别标有A1,A2两个点(如图所示),经过t秒A1,A2两个点运动到新位置B1,B2,设B1,B2到水平线O1O2的垂直高度(当A1,A2运动到水平线O1O2下方时,高度是负值)分别是h1,h2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com