
分析 (Ⅰ)利用正弦定理化简已知条件,然后通过余弦定理求出角A的大小,然后通过数量积化简求出三角形的面积.
(Ⅱ)由已知结合(Ⅰ)可求a1,利用等比数列的性质可求d,求出通项公式,利用错位相减法求出数列{bn}的前n项和为Tn,再确定Tn取值范围,解不等式即可得解.
解答 (本题满分为14分)
解:(I)由正弦定理得:$\frac{b}{a+c}=1-\frac{c}{a+b}$即:b2+c2-a2=bc,
所以由余弦定理得:$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{bc}{2bc}=\frac{1}{2}$,
又因为:0<A<π,所以$A=\frac{π}{3}$,…3分
因为$b=5,\overrightarrow{CA}•\overrightarrow{CB}=-5$,即:5acosC=-5,即:$5a\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=-5$
与$cos\frac{π}{3}=\frac{{25+{c^2}-{a^2}}}{10c}$,联立解得:c=12,…5分
所以△ABC的面积是:$\frac{1}{2}×5×12×sinA=15\sqrt{3}$,…6分
(Ⅱ)数列{an}的公差为d,且d≠0,由a1cosA=1得a1=2,
又a2,a4,a8成等比数列,得${a_4}^2={a_2}•{a_8}$,解得d=2,…8分
所以an=2+(n-1)×2=2n,${b_n}=\frac{a_n}{2^n}=\frac{n}{{{2^{n-1}}}}$,
∵Tn=1×($\frac{1}{2}$)0+2×($\frac{1}{2}$)1+…+n×($\frac{1}{2}$)n-1①,
∴$\frac{1}{2}$Tn=1×($\frac{1}{2}$)1+2×($\frac{1}{2}$)2+…+n×($\frac{1}{2}$)n,②
①-②得$\frac{1}{2}$Tn=1+$\frac{1}{2}$+…+($\frac{1}{2}$)n-1-n×($\frac{1}{2}$)n,
∴Tn=4[1-($\frac{1}{2}$)n]-n×($\frac{1}{2}$)n-1,
=4-4×($\frac{1}{2}$)n-n×($\frac{1}{2}$)n-1=4-(2n+4)($\frac{1}{2}$)n.易知Tn<4,
又Tn+1-Tn=4-(2n+6)($\frac{1}{2}$)n+1-4+(2n+4)($\frac{1}{2}$)n=(n+1)•($\frac{1}{2}$)n>0,
所以Tn≥T1=1,即1≤Tn<4
假设存在正整数m,使得m+1≤Tn<m+3对任意正整数n恒成立.
则$\left\{\begin{array}{l}m+1≤1\\ m+3≥4\end{array}\right.⇒\left\{\begin{array}{l}m≤0\\ m≥1\end{array}\right.$这不可能,故,m不存在.…14分
点评 本题主要考查了余弦定理以及正弦定理的应用,三角形的面积的求法,等差数列与等比数列的综合,考查数列的通项与求和,考查数列的单调性,正确求数列的通项与求和是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
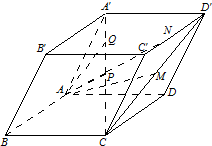 如图,在平行六面体ABCD-A′B′C′D′中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{AA'}=\overrightarrow c$,P是CA′的中点,M是CD′的中点,N是C′D′的中点,点Q在CA′上,且CQ:QA′=4:1,试用基向量$\{\overrightarrow a,\overrightarrow{b},\overrightarrow c\}$表示以下向量:
如图,在平行六面体ABCD-A′B′C′D′中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{AA'}=\overrightarrow c$,P是CA′的中点,M是CD′的中点,N是C′D′的中点,点Q在CA′上,且CQ:QA′=4:1,试用基向量$\{\overrightarrow a,\overrightarrow{b},\overrightarrow c\}$表示以下向量:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com