
某汽车厂生产的A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| | 轿车A | 轿车B | 轿车C |
| 舒适性 | 800 | 450 | 200 |
| 标准型 | 100 | 150 | 300 |
(Ⅰ)100;(Ⅱ)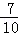 ;(Ⅲ)
;(Ⅲ) .
.
解析试题分析:(Ⅰ)利用分层抽样满足每个个体被抽到的概率相等,建立等式,即可求抽取的轿车的数量n.
(Ⅱ)先利用分层抽样满足每个个体被抽到的概率相等,求出抽取一个容量为5的样本舒适型轿车的辆数,利用列举的方法求出至少有1辆舒适型轿车的基本事件,利用古典概型的概率公式求出概率.
(Ⅲ)先求出总体平均数,再总体平均数数之差的绝对值超过0.6的是8.2和9.6这2个数,利用古典概型的概率公式求出概率.
试题解析:(Ⅰ)由题意得,轿车的总数为800+100+450+150+200+300=2000,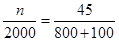 ,解得n=100;
,解得n=100;
(Ⅱ)设抽取的样本中有m辆舒适型轿车,则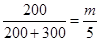 ,解得m=2,也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,
,解得m=2,也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,
则从中任取2辆的所有基本事件为(S1,B1),(S1,B2),(S1,B3) (S2,B1),(S2,B2),(S2,B3),(S1,S2),(B1,B2),(B2,B3),(B1,B3)共10个;
其中至少有1辆舒适型轿车的基本事件有7个基本事件:(S1,B1),(S1,B2),(S1,B3) (S2,B1),(S2,B2),(S2,B3),(S1,S2),共7个;
所以从中任取2辆,至少有1辆舒适型轿车的概率为P=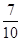 ,
,
(Ⅲ)总体平均数为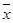 =
=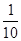 (8.7+9.3+8.2+9.4+8.6+9.2+9.6+9.0+8.4+8.6)=8.9,则该数与总体平均数之差的绝对值超过0.6的有8.2和9.6,共2个;
(8.7+9.3+8.2+9.4+8.6+9.2+9.6+9.0+8.4+8.6)=8.9,则该数与总体平均数之差的绝对值超过0.6的有8.2和9.6,共2个;
故该数与总体平均数之差的绝对值超过0.6的概率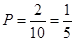 .
.
考点:1.分层抽样;2.求古典概型的事件的概率公式;3.频率分布表.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
 .
.
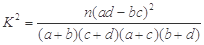 ,其中
,其中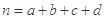 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从某校高三上学期期末数学考试成绩中,随机抽取了 名学生的成绩得到频率分布直方图如下图所示:
名学生的成绩得到频率分布直方图如下图所示: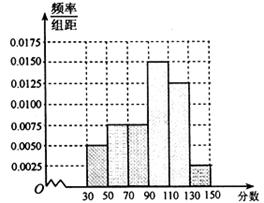
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分(平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和);
(2)若用分层抽样的方法从分数在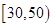 和
和 的学生中共抽取
的学生中共抽取 人,该
人,该 人中成绩在
人中成绩在 的有几人?
的有几人?
(3)在(2)中抽取的 人中,随机抽取
人中,随机抽取 人,求分数在
人,求分数在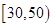 和
和 各
各 人的概率.
人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了估计某产品寿命的分布,对产品进行追踪调查,记录如下:
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下
表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文
科学生总成绩不好与数学成绩不好有关系吗?
| | 总成绩好 | 总成绩不好 | 总计 |
| 数学成绩好 | 20 | 10 | 30 |
| 数学成绩不好 | 5 | 15 | 20 |
| 总计 | 25 | 25 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的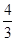 倍.
倍.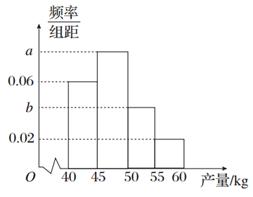
(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树中随机抽取2株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a= 。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用 分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为 。
分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为 。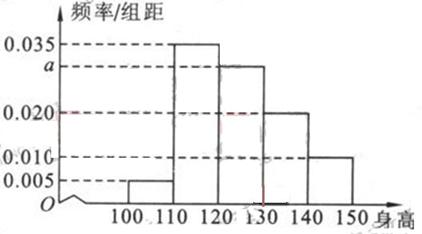
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
某校高中年级开设了丰富多彩的校本课程,甲、乙两班各随机抽取了5名学生的学分,用茎叶图表 示(如右图).
示(如右图). ,
,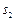 分别表示甲、乙两班各自5名学生学分的标准差,则
分别表示甲、乙两班各自5名学生学分的标准差,则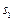
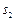 .(填“
.(填“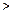 ”、“
”、“ ”或“=”)
”或“=”) 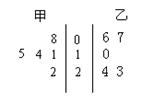
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
某单位为了了解用电量y(度)与气温x(°C)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
| 气温(°C) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
 当气温为-4°C时,预测用电量的度数约为
当气温为-4°C时,预测用电量的度数约为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com