
分析 由题意可得△ABC是以∠C为直角的直角三角形,然后根据已知条件把$\overrightarrow{CD}、\overrightarrow{CE}$用向量$\overrightarrow{CA}、\overrightarrow{CB}$表示,则$\overrightarrow{CD}•\overrightarrow{CE}$的值可求.
解答 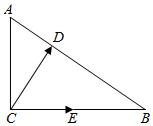 解:在△ABC中,由AC=3,BC=4,AB=5,得AC2+BC2=AB2,
解:在△ABC中,由AC=3,BC=4,AB=5,得AC2+BC2=AB2,
∴△ABC是以∠C为直角的直角三角形,如图,
∵$\overrightarrow{BE}=\frac{1}{2}\overrightarrow{BC}$,∴$\overrightarrow{CE}=\frac{1}{2}\overrightarrow{CB}$,
又$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}$,∴$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}=\overrightarrow{CA}+\frac{1}{3}\overrightarrow{AB}=\overrightarrow{CA}$$+\frac{1}{3}(\overrightarrow{CB}-\overrightarrow{CA})$
=$\frac{1}{3}\overrightarrow{CB}+\frac{2}{3}\overrightarrow{CA}$,
∴$\overrightarrow{CD}•\overrightarrow{CE}$=$(\frac{1}{3}\overrightarrow{CB}+\frac{2}{3}\overrightarrow{CA})•\frac{1}{2}\overrightarrow{CB}$=$\frac{1}{6}|\overrightarrow{CB}{|}^{2}+\frac{1}{3}\overrightarrow{CA}•\overrightarrow{CB}=\frac{1}{6}×{4}^{2}=\frac{8}{3}$.
故答案为:$\frac{8}{3}$.
点评 本题考查平面向量的数量积运算,考查了向量的数乘、加法法则与减法法则,是中档题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{25}$ | B. | $\frac{8}{25}$ | C. | $\frac{17}{25}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值9 | B. | 最大值9 | C. | 最小值4 | D. | 最大值4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
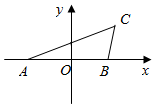 如图,A(-2,0),B(2,0),第一象限内点C满足∠ACB=60°,且△ABC的面积为$\sqrt{3}$.双曲线Г以A、B为焦点,经过点C.
如图,A(-2,0),B(2,0),第一象限内点C满足∠ACB=60°,且△ABC的面积为$\sqrt{3}$.双曲线Г以A、B为焦点,经过点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com