
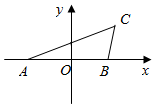
 如图,A(-2,0),B(2,0),第一象限内点C满足∠ACB=60°,且△ABC的面积为$\sqrt{3}$.双曲线Г以A、B为焦点,经过点C.
如图,A(-2,0),B(2,0),第一象限内点C满足∠ACB=60°,且△ABC的面积为$\sqrt{3}$.双曲线Г以A、B为焦点,经过点C.分析 (1)设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),由题意可得c=2,运用三角形的面积公式和余弦定理,可得|AC|-|BC|=2$\sqrt{3}$,再由双曲线的定义可得a,求得b,进而得到双曲线的方程;
(2)运用等差数列的中项的性质和双曲线的定义,可得|MN|=4$\sqrt{3}$,设出直线l的方程,联立双曲线的方程,运用韦达定理和弦长公式,解方程可得k,进而得到所求直线的方程.
解答 解:(1)设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),
由题意可得c=2,$\frac{1}{2}$|AC|•|BC|sin60°=$\sqrt{3}$,即|AC|•|BC|=4,
又|AB|2=|AC|2+|BC|2-2|AC|•|BC|cos60°,
即为16=(|AC|-|BC|)2+|AC|•|BC|,
可得(|AC|-|BC|)2=16-4=12,
即为|AC|-|BC|=2$\sqrt{3}$,
由双曲线的定义可得2a=2$\sqrt{3}$,即a=$\sqrt{3}$,b=$\sqrt{{c}^{2}-{a}^{2}}$=1,
则双曲线的方程为$\frac{{x}^{2}}{3}$-y2=1;
(2)由双曲线的定义可得|AM|-|BM|=|AN|-|BN|=2a=2$\sqrt{3}$,
可得|AM|+|AN|=4a+|BM|+|BN|=4$\sqrt{3}$+|MN|,
由|AM|、|MN|、|AN|成等差数列,可得|AM|+|AN|=2|MN|,
即有|MN|=4$\sqrt{3}$,
设过点B的直线的方程为y=k(x-2),
代入双曲线的方程x2-3y2=3,可得(1-3k2)x2+12k2x-12k2-3=0,
设M(x1,y1),N(x2,y2),则x1+x2=-$\frac{12{k}^{2}}{1-3{k}^{2}}$,x1x2=-$\frac{12{k}^{2}+3}{1-3{k}^{2}}$,
由弦长公式可得|MN|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{144{k}^{4}}{(1-3{k}^{2})^{2}}+\frac{48{k}^{2}+12}{1-3{k}^{2}}}$=4$\sqrt{3}$,
即为1+k2=2(3k2-1),
解得k=±$\frac{\sqrt{15}}{5}$,
即有直线l的方程为y=±$\frac{\sqrt{15}}{5}$(x-2).
点评 本题考查双曲线的方程的求法,注意运用三角形的面积公式和余弦定理,结合双曲线的定义,考查直线的方程的求法,注意运用双曲线的定义和等差数列的中项的性质,联立直线和双曲线的方程,运用韦达定理和弦长公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$±\frac{\sqrt{3}}{3}$x | B. | y=$±\sqrt{3}$x | C. | y=±x | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知PA与⊙O相切,A为切点,PBC为割线,D为⊙O上一点,AD、BC相交于点E.
如图,已知PA与⊙O相切,A为切点,PBC为割线,D为⊙O上一点,AD、BC相交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,且以坐标原点为圆心,椭圆的短半轴长为半径的圆与直线$x-y+\sqrt{2}=0$相切.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,且以坐标原点为圆心,椭圆的短半轴长为半径的圆与直线$x-y+\sqrt{2}=0$相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com