
 ��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��a��b��0��$��������Ϊ$\frac{{\sqrt{3}}}{2}$����������ԭ��ΪԲ�ģ���Բ�Ķ̰��᳤Ϊ�뾶��Բ��ֱ��$x-y+\sqrt{2}=0$���У�
��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��a��b��0��$��������Ϊ$\frac{{\sqrt{3}}}{2}$����������ԭ��ΪԲ�ģ���Բ�Ķ̰��᳤Ϊ�뾶��Բ��ֱ��$x-y+\sqrt{2}=0$���У����� ��1������Բ��������Ϊ$\frac{{\sqrt{3}}}{2}$��������ԭ��ΪԲ�ģ���Բ�Ķ̰��᳤Ϊ�뾶��Բ��ֱ��$x-y+\sqrt{2}=0$���У����a��b���ɴ��������ԲC�ķ��̣�
��2����ֱ��l�ķ���Ϊy=kx+m��A��x1��y1����B��x2��y2����������Բ���̣��ã�1+4k2��x2+8kmx+4m2-4=0���ɴ�����Τ�ﶨ���������б�ʽ���ȱ����С���Բ���ʣ��������֪���������|OA|2+|OB|2��ֵ��
��� �⣺��1������Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��a��b��0��$��������Ϊ$\frac{{\sqrt{3}}}{2}$��
��������֪e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$����e2=$\frac{{c}^{2}}{{a}^{2}}=\frac{\sqrt{{a}^{2}-{b}^{2}}}{{a}^{2}}$=$\frac{3}{4}$��
��������a2=4b2����a=2b��
�֡�������ԭ��ΪԲ�ģ���Բ�Ķ̰��᳤Ϊ�뾶��Բ��ֱ��$x-y+\sqrt{2}=0$���У�
��b=$\frac{\sqrt{2}}{\sqrt{1+1}}$=1����a=2��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{4}+{y}^{2}$=1��
��2����ֱ��l�ķ���Ϊy=kx+m��A��x1��y1����B��x2��y2����
��ֱ��l�ķ��̴�����Բ���̣���ȥy�ã���1+4k2��x2+8kmx+4m2-4=0��
��x1+x2=-$\frac{8km}{1+4{k}^{2}}$��x1x2=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$���ҡ�=16��1+4k2-m2����0��
��k1��k��k2ǡ�ù��ɵȱ����У�
��k2=k1k2=$\frac{��k{x}_{1}+m����k{x}_{2}+m��}{{x}_{1}{x}_{2}}$��
��-4k2m2+m2=0��
��k=��$\frac{1}{2}$��
��ʱ��=16��2-m2����0����m�ʣ�-$\sqrt{2}$��$\sqrt{2}$����
��x1+x2=��2m��x1x2=2m2-2
��|OA|2+|OB|2=${{x}_{1}}^{2}+{{y}_{1}}^{2}+{{x}_{2}}^{2}+{{y}_{2}}^{2}$=$\frac{3}{4}$[��x1+x2��2-2x1x2]+2=5��
��|OA|2+|OB|2�Ƕ�ֵΪ5��
���� ���⿼����Բ���̵������������Ϊ��ֵ�������е��⣬����ʱҪ�������⣬ע��Τ�ﶨ���������б�ʽ���ȱ����С���Բ���ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
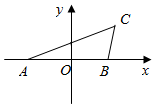 ��ͼ��A��-2��0����B��2��0������һ�����ڵ�C�����ACB=60�㣬�ҡ�ABC�����Ϊ$\sqrt{3}$��˫���ߧ���A��BΪ���㣬������C��
��ͼ��A��-2��0����B��2��0������һ�����ڵ�C�����ACB=60�㣬�ҡ�ABC�����Ϊ$\sqrt{3}$��˫���ߧ���A��BΪ���㣬������C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8��$\frac{f��2��}{f��1��}$��16 | B�� | 4��$\frac{f��2��}{f��1��}$��8 | C�� | 3��$\frac{f��2��}{f��1��}$��4 | D�� | 2��$\frac{f��2��}{f��1��}$��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
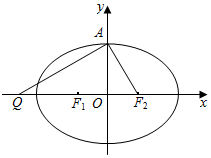 ����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2���϶���ΪA������A��AF2��ֱ��ֱ�߽�x�Ḻ�����ڵ�Q����F1ǡ��QF2���е㣮����A��Q��F2�����Բǡ����ֱ��l��x-$\sqrt{3}$y-3=0���У�
����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2���϶���ΪA������A��AF2��ֱ��ֱ�߽�x�Ḻ�����ڵ�Q����F1ǡ��QF2���е㣮����A��Q��F2�����Բǡ����ֱ��l��x-$\sqrt{3}$y-3=0���У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com