
| A. | y=$±\frac{\sqrt{3}}{3}$x | B. | y=$±\sqrt{3}$x | C. | y=±x | D. | y=±2x |
分析 由对称性可得MN过原点O,可得MF⊥NF,运用正切函数的定义和双曲线的定义,求得MF,NF,再由勾股定理和渐近线方程即可得到所求.
解答 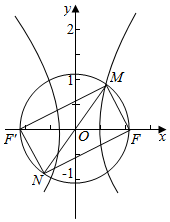 解:由对称性可得MN过原点O,可得
解:由对称性可得MN过原点O,可得
MF⊥NF,即有tan∠MNF=$\frac{|MF|}{|NF|}$=tan$\frac{π}{12}$=2-$\sqrt{3}$,
由双曲线的定义可得|NF|-|MF|=|MF'|-|MF|=2a,
解得|MF|=($\sqrt{3}$-1)a,|NF|=($\sqrt{3}$+1)a,
在直角三角形MFF'中,由勾股定理可得,
4c2=($\sqrt{3}$-1)2a2+($\sqrt{3}$+1)2a2,
即为c2=2a2,即有b2=c2-a2=a2,
则双曲线的渐近线方程为y=±$\frac{b}{a}$x,
即y=±x.
故选:C.
点评 本题考查双曲线的渐近线方程求法,注意运用双曲线的定义和对称性,以及直径所对的圆周角为直角,正切函数的定义,考查化简整理的运算能力,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 最小值9 | B. | 最大值9 | C. | 最小值4 | D. | 最大值4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{π}{4}$ | C. | -$\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
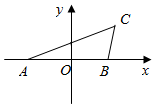 如图,A(-2,0),B(2,0),第一象限内点C满足∠ACB=60°,且△ABC的面积为$\sqrt{3}$.双曲线Г以A、B为焦点,经过点C.
如图,A(-2,0),B(2,0),第一象限内点C满足∠ACB=60°,且△ABC的面积为$\sqrt{3}$.双曲线Г以A、B为焦点,经过点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知⊙C1:(x+$\sqrt{6}$)2+y2=32及点C2($\sqrt{6}$,0),在⊙C1上任取一点P,连结C2P,作线段C2P的中垂线交直线C1P于点M.
如图,已知⊙C1:(x+$\sqrt{6}$)2+y2=32及点C2($\sqrt{6}$,0),在⊙C1上任取一点P,连结C2P,作线段C2P的中垂线交直线C1P于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8<$\frac{f(2)}{f(1)}$<16 | B. | 4<$\frac{f(2)}{f(1)}$<8 | C. | 3<$\frac{f(2)}{f(1)}$<4 | D. | 2<$\frac{f(2)}{f(1)}$<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com