
分析 (1)将f(x)=x代入定义(x+T)=T f(x)验证,即可知函数f(x)=x不属于集合M;
(2)将-3<x<-2转化为1<x+4<2,利用当1<x<2时,f(x)=x+lnx,即可求得f(x+4)的解析式,再利用f(x+T)=Tf(x),即可求得f(x)的解析式;
(3)若函数f(x)=sinkx∈M,依据定义应该有sin(kx+kT)=Tsinkx∈[-1,1]对任意实数都成立,故T=±1.将T=±1代入sin(kx+kT)=Tsinkx求k的范围即可.
解答 解:(1)∵函数f(x)=x,
∴对于非零常数T,f(x+T)=x+T,Tf(x)=Tx,
∵集合M是满足下列性质的函数f(x)的全体:
存在非零常数T,使得对任意x∈R,有f(x+T)=Tf(x)成立,
而对任意x∈R,x+T=Tx,不能恒成立,
∴不满足上述性质,
∴f(x)=x∉M;
(2)∵-3<x<-2,
∴1<x+4<2,
∴f(x+4)=x+4+ln(x+4),
∵存在非零常数T,使得对任意x∈R,有f(x+T)=Tf(x)成立,
∴令T=2,
∴f(x+4)=f[(x+2)+2]=2f(x+2)=4f(x),
∴f(x)=$\frac{1}{4}$[x+4+ln(x+4)],
∴当-3<x<-2时,f(x)的解析式是f(x)=$\frac{1}{4}$[x+4+ln(x+4)].
(3)当k=0时,f(x)=0,显然f(x)=0∈M.
当k≠0时,因为f(x)=sinkx∈M,所以存在非零常数T,
对任意x∈R,有f(x+T)=Tf(x)成立,
即sin(kx+kT)=Tsinkx.
因为k≠0,且x∈R,所以kx∈R,kx+kT∈R,
于是sinkx∈[-1,1],sin(kx+kT)∈[-1,1],
故要使sin(kx+kT)=Tsinkx.成立,
只有T=±1,当T=1时,sin(kx+k)=sinkx成立,
则k=2mπ,m∈Z.
当T=-1时,sin(kx-k)=-sinkx成立,
即sin(kx-k+π)=sinkx成立,
则-k+π=2mπ,m∈Z,即k=-(2m-1)π,m∈Z.
综合得,实数k的取值范围是{k|k=mπ,m∈Z}.
点评 本题考查了抽象函数及其应用,函数解析式的求解及常用方法,考查新定义下问题的证明与求解,此类题的特点是探究时只能以新定义的规则为依据,不能引入熟悉的算法,这是做此类题时要注意的.


科目:高中数学 来源: 题型:选择题
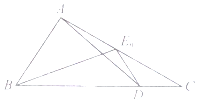 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BC}=3\overrightarrow{DC}$,${E_n}(n∈{N^*})$为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)•\overrightarrow{{E_n}D}$,其中实数列{an}中,an>0,a1=1,则a5=( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BC}=3\overrightarrow{DC}$,${E_n}(n∈{N^*})$为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)•\overrightarrow{{E_n}D}$,其中实数列{an}中,an>0,a1=1,则a5=( )| A. | 46 | B. | 30 | C. | 242 | D. | 161 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5,10) | B. | (10,20) | C. | [20,+∞) | D. | (5,10)∪[20,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com