
分析 (1)利用椭圆的离心率e=$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1、F2,点P(2,$\sqrt{3}$),点F2在线段PF1的中垂线上,求出几何量,即可得到椭圆的方程;
(2)设出直线l1,l2的方程,与椭圆方程联立,利用根的判别式,即可确定l1的斜率k的取值范围;
(3)利用韦达定理,确定M,N的坐标,分类讨论,确定直线MN的方程,即可得到结论.
解答 解:(1)由椭圆E的离心率e=$\frac{\sqrt{2}}{2}$得$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
∵点F2在线段PF1的中垂线上,∴|F1F2|=|PF2|
∵F1(-c,0),F2(c,0)
∴$(2c)^{2}=(2-c)^{2}+(\sqrt{3})^{2}$
解得c=1,a2=2,b2=1
∴椭圆E的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)由题意知,直线l1的斜率存在并不为零,
∴l1:y=k(x-$\frac{3}{2}$),∴l2:y=-$\frac{1}{k}$(x-$\frac{3}{2}$)
由y=k(x-$\frac{3}{2}$),代入椭圆方程消去y并化简整理,得(1+2k2)x2-6k2x+$\frac{9}{2}$k2-2=0,
根据题意,△>0,∴k2<4
同理$(-\frac{1}{k})^{2}$<4,∴k2>$\frac{1}{4}$
∴$\frac{1}{4}$<k2<4
∴k∈(-2,-$\frac{1}{2}$)∪($\frac{1}{2}$,2);
(3)设A(x1,y1),B(x2,y2),M(x0,y0),则x1+x2=$\frac{6{k}^{2}}{1+2{k}^{2}}$
∴x0=$\frac{3{k}^{2}}{1+2{k}^{2}}$
∴y0=-$\frac{3k}{2(1+2{k}^{2})}$
∴M($\frac{3{k}^{2}}{1+2{k}^{2}}$,-$\frac{3k}{2(1+2{k}^{2})}$)
同理N($\frac{3}{{k}^{2}+2}$,$\frac{3k}{2({k}^{2}+2)}$)
①当k2=1时,直线MN的方程为x=1;
②当k2≠1时,直线MN的斜率为kMN=$\frac{3k}{2(1-{k}^{2})}$
∴直线MN的方程为y+$\frac{3k}{2(1+2{k}^{2})}$=$\frac{3k}{2(1-{k}^{2})}$(x-$\frac{3{k}^{2}}{1+2{k}^{2}}$)
化简可得y=$\frac{3k}{2(1-{k}^{2})}$(x-1),此直线恒过定点K(1,0)
综合①②知,直线MN恒过定点K(1,0).
点评 本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查直线恒过定点,考查学生分析解决问题的能力,正确运用韦达定理是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{{\sqrt{2}}}{2}$,1) | C. | (0,$\frac{1}{2}$] | D. | (0,$\frac{{\sqrt{2}}}{2}}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.
如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
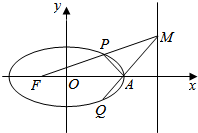 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左焦点为F(-1,0),M为右准线x=4上的一动点(不在x轴上),线段FM交椭圆于点P,MA与椭圆的另一交点为Q.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左焦点为F(-1,0),M为右准线x=4上的一动点(不在x轴上),线段FM交椭圆于点P,MA与椭圆的另一交点为Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y-8=0 | B. | 2x-y-8=0 | C. | x+2y-4=0 | D. | 2x-y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com