
分析 (1)由题意可设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),由于直线l过点(1,2),代入直线方程,利用基本不等式即可得出ab的最小值,取得最小值时a,b,即可得到A,B的坐标,进而得到椭圆M的方程;
(2)讨论直线CD的斜率不存在和存在两种情况,求出CD的弦长,再由面积公式,比较,即可得到最大值,进而得到k,从而得到直线方程.
解答 解:(1)由题意可设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),
∵直线l过点(1,2),
∴$\frac{1}{a}$+$\frac{2}{b}$=1.
∴1=$\frac{1}{a}$+$\frac{2}{b}$≥2$\sqrt{\frac{2}{ab}}$,∴ab≥8,当且仅当$\frac{1}{a}$=$\frac{2}{b}$,即a=2,b=4是取等号.
此时△AOB的面积取得最小值$\frac{1}{2}$ab=4,
直线l的方程为$\frac{x}{2}$+$\frac{y}{4}$=1.
此时A(2,0),B(0,4),
由于A、B两点恰好是椭圆M:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>0,n>0)的顶点,
即有m=2,n=4,即有椭圆M的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{16}$=1;
(2)当直线CD的斜率不存在时,即方程x=1,
代入曲线方程,解得,y=±2$\sqrt{3}$,
即有CD=4$\sqrt{3}$,A,B到直线CD的距离为1,四边形ACBD面积为$\frac{1}{2}$×2×4$\sqrt{3}$=4$\sqrt{3}$;
当k存在时,设直线CD:y-2=k(x-1),即y=kx+2-k,
代入曲线方程,可得,(4+k2)x2+2k(2-k)x+(2-k)2-16=0,
由于有两个交点,则判别式△=[2k(2-k)]2-4(4+k2)[(2-k)2-16]>0,
解得k∈R,
且x1+x2=$\frac{2k(k-2)}{4+{k}^{2}}$,x1x2=$\frac{(2-k)^{2}-16}{4+{k}^{2}}$,
则四边形ACBD的面积=$\frac{1}{2}$•2•$\frac{|k+2|}{\sqrt{1+{k}^{2}}}$•$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{4{k}^{2}(k-2)^{2}}{(4+{k}^{2})^{2}}-\frac{4(2-k)^{2}-64}{4+{k}^{2}}}$
=4$\sqrt{\frac{({k}^{2}+4k+4)(3{k}^{2}+4k+12)}{(4+{k}^{2})^{2}}}$=4$\sqrt{3+\frac{16{k}^{2}}{(4+{k}^{2})^{2}}+\frac{16k}{4+{k}^{2}}}$,
令t=$\frac{k}{4+{k}^{2}}$,要求最大值,则k>0,则有t=$\frac{1}{k+\frac{4}{k}}$≤$\frac{1}{4}$,
即有S=4$\sqrt{3+16{t}^{2}+16t}$≤4$\sqrt{3+1+4}$=8$\sqrt{2}$.
则有四边形ACBD面积的最大值为8$\sqrt{2}$,此时k=2.
故四边形ABCD面积最大时,直线l的方程为y=2x.
点评 本题考查直线方程的点斜式和截距式的运用,基本不等式的运用:求最值,考查四边形的面积的求法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的顶点为A1,A2,B1B2,焦点为F1,F2,a2+b2=7
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的顶点为A1,A2,B1B2,焦点为F1,F2,a2+b2=7查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 483 | B. | 482 | C. | 481 | D. | 480 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 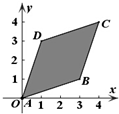 | B. | 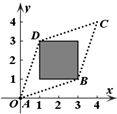 | C. | 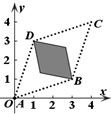 | D. | 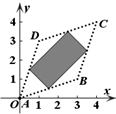 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com