
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
分析 如图,试验的所有基本事件所构成的区域为矩形OABC及其内部,利用一元二次方程根的判别式算出方程有实根的事件对应的区域为图中的三角形OAD及其内部,求出两个区域的面积并利用几何概型公式,即可算出所求的概率.
解答 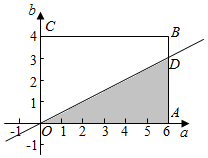 解:如图,所有的基本事件对应集合Ω={(a,b)|0≤a≤6,0≤b≤4},
解:如图,所有的基本事件对应集合Ω={(a,b)|0≤a≤6,0≤b≤4},
构成的区域为如图的矩形OABC及其内部,其面积为S=6×4=24;
设事件A=“方程x2-ax+b2=0有实根”,
∵△=(a)2-4×1×b2≥0,结合a、b都是非负数,解得a≥2b,
∴事件A对应的集合A={(a,b)|0≤a≤6,0≤b≤4,且a≥2b},
所构成的区域为矩形OABC及其内部,且在直线a=2b的右下方部分,
即图中的三角形OAD及其内部,其面积S'=$\frac{1}{2}$×6×3=9.
由于点(a,b)落在区域内的每一点是随机的,
∴事件A发生的概率P(A)=$\frac{9}{24}$=$\frac{3}{8}$,即方程有实根的概率是$\frac{3}{8}$.
故选:C.
点评 本题给出含有字母参数的一元二次方程,求方程有实数根的概率.着重考查了一元二次方程根的判别式、不等式表示的平面区域、面积公式和几何概型计算公式等知识,属于中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
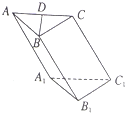 如图:在三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,且与C在
如图:在三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,且与C在查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com