
| A. | $\frac{3}{4}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 根据椭圆的定义,结合|PF1|=3|PF2|,求出|PF1|=3,|PF2|=1,利用余弦定理,即可求cos∠F1PF2的值.
解答 解:由椭圆C:$\frac{x^2}{4}+{y^2}$=1,得a2=4,b2=1,
则$a=2,c=\sqrt{{a}^{2}-{b}^{2}}=\sqrt{3}$,
设|PF1|=3|PF2|=3m,则根据椭圆的定义,可得3m+m=4,∴m=1,
∴|PF1|=3,|PF2|=1,
∵|F1F2|=2c=$2\sqrt{3}$.
∴cos∠F1PF2=$\frac{{3}^{2}+{1}^{2}-(2\sqrt{3})^{2}}{2×3×1}=-\frac{1}{3}$.
故选:B.
点评 本题考查椭圆的性质,考查椭圆的定义,考查余弦定理的运用,属于中档题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
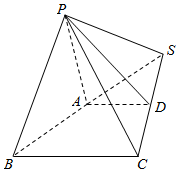 在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC.
在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 30° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{2}$+y2=1 | B. | $\frac{x^2}{3}$+$\frac{y^2}{2}$=1 | C. | $\frac{x^2}{4}$+y2=1 | D. | $\frac{x^2}{4}$+$\frac{y^2}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com