
分析 (Ⅰ)由题意可得:$\left\{\begin{array}{l}{a=\sqrt{3}b}\\{2×\frac{1}{2}×2a×b=2\sqrt{3}}\end{array}\right.$,解得a,b,即可得出.
(II)(1)当l的斜率不存在时,A,B两点关于x轴对称,则x1=x2,y1=-y2,由A(x1,y1)在椭圆上,则$\frac{{{x_1}^2}}{3}+{y_1}^2=1$,而$S=|{x_1}{y_1}|=\frac{{\sqrt{3}}}{2}$,解出即可得出|OC|.
(2)当l的斜率存在时,设直线l:y=kx+m,与椭圆方程联立可得:(3k2+1)x2+6kmx+3m2-3=0,由△>0,得m2<3k2+1,|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,原点O到直线l的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,△OAB的面积S=$\frac{1}{2}$|AB|d=$\frac{\sqrt{3}}{2}$,整理为(3k2+1)2-4m2(3k2+1)+4m4=0,利用中点坐标公式可得C,再利用两点之间的距离公式及其二次函数的单调性即可得出|OC|的取值范围.
解答 解:(Ⅰ)由题意可得:$\left\{\begin{array}{l}{a=\sqrt{3}b}\\{2×\frac{1}{2}×2a×b=2\sqrt{3}}\end{array}\right.$,解得a=$\sqrt{3}$,b=1,
∴椭圆E的方程为:$\frac{{x}^{2}}{3}+{y}^{2}$=1.
(Ⅱ)(1)当l的斜率不存在时,A,B两点关于x轴对称,则x1=x2,y1=-y2,
由A(x1,y1)在椭圆上,则$\frac{{{x_1}^2}}{3}+{y_1}^2=1$,而$S=|{x_1}{y_1}|=\frac{{\sqrt{3}}}{2}$,解得$|{x_1}|=\frac{{\sqrt{6}}}{2}$,$|{y_1}|=\frac{{\sqrt{2}}}{2}$,
可知$C(±\frac{{\sqrt{6}}}{2},0)$,∴$|OC|=\frac{{\sqrt{6}}}{2}$.
(2)当l的斜率存在时,设直线l:y=kx+m,
联立方程组$\left\{\begin{array}{l}\frac{x^2}{3}+{y^2}=1\\ y=kx+m\end{array}\right.$消去y得(3k2+1)x2+6kmx+3m2-3=0,
由△=12(3k2-m2+1)>0,得m2<3k2+1,
则${x_1}+{x_2}=\frac{-6km}{{3{k^2}+1}}$,${x_1}{x_2}=\frac{{3{m^2}-3}}{{3{k^2}+1}}$,(*)
|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$$•\frac{2\sqrt{3}\sqrt{3{k}^{2}-{m}^{2}+1}}{3{k}^{2}+1}$,
原点O到直线l的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,
△OAB的面积$S=\frac{1}{2}|AB|•d=\frac{1}{2}\sqrt{1+{k^2}}•\frac{{2\sqrt{3}\sqrt{3{k^2}-{m^2}+1}}}{{3{k^2}+1}}•\frac{|m|}{{\sqrt{1+{k^2}}}}=\frac{{\sqrt{3}}}{2}$,
整理得4m2(3k2+1-m2)=(3k2+1)2,即(3k2+1)2-4m2(3k2+1)+4m4=0,
∴(3k2+1-2m2)2=0,即2m2=3k2+1,满足△=12(3k2-m2+1)>0,
可知2m2≥1,
结合(*)得${x_1}+{x_2}=\frac{-3k}{m}$,${y_1}+{y_2}=k({x_1}+{x_2})+2m=\frac{{-3{k^2}}}{m}+2m=\frac{{-(2{m^2}-1)}}{m}+2m=\frac{1}{m}$,
则C$(-\frac{3k}{2m},\frac{1}{2m})$,∴$|OC{|^2}=\frac{{9{k^2}+1}}{{4{m^2}}}=\frac{{3(2{m^2}-1)+1}}{{4{m^2}}}=\frac{3}{2}-\frac{1}{{2{m^2}}}$,
由于2m2≥1,则$|OC{|^2}≥\frac{1}{2}$,当且仅当2m2=1,即k=0时,等号成立,故$|OC|≥\frac{{\sqrt{2}}}{2}$,
综上所述,|OC|的最小值为$\frac{{\sqrt{2}}}{2}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、三角形与矩形面积计算公式、不等式的性质,考查了分类讨论方法、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{15}{28}$ | D. | $\frac{19}{28}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
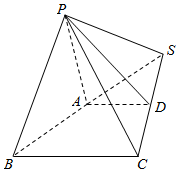 在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC.
在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
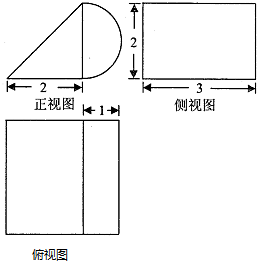
| A. | 4+$\frac{2}{3}π$ | B. | 4+$\frac{3}{2}$π | C. | 6+$\frac{2}{3}π$ | D. | 6+$\frac{3}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 30° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com