
直线y=kx+m(m≠0)与椭圆W: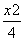 +y2=1相交于A,C两点,O是坐标原点.
+y2=1相交于A,C两点,O是坐标原点.
(1)当点B的坐标为(0,1),且四边形OABC为菱形时,求AC的长;
(2)当点B在W上且不是W的顶点时,证明:四边形OABC不可能为菱形.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
若a、b是正常数,a≠b,x,y∈(0,+∞),则 ,当且仅当
,当且仅当 =
= 时上式取等号.利用以上结论,可以得到函数f(x)=
时上式取等号.利用以上结论,可以得到函数f(x)= +
+ (x∈(0,
(x∈(0, ))的最小值为________.
))的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明:若整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,那么a、b、c中至少有一个是偶数.用反证法证明时,下列假设正确的是( )
A.假设a,b,c都是偶数
B.假设a,b,c都不是偶数
C.假设a,b,c至多有一个偶数
D.假设a,b,c至多有两个偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,把1,3,6,10,15,21,…这些数叫作三角形数,这是因为这些数目的点可以排成一个正三角形,试求第七个三角形数是( )
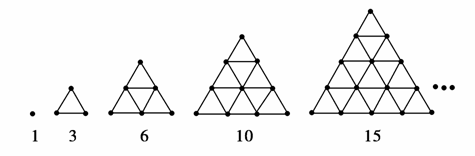
A.27 B.28
C.29 D.30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com