
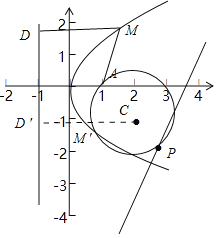
【题目】在平面直角坐标系xOy中,点A(1,0),动点M满足以MA为直径的圆与y轴相切.过A作直线x+(m﹣1)y+2m﹣5=0的垂线,垂足为B,则|MA|+|MB|的最小值为( )
A.2![]() B.2
B.2![]() C.
C.![]() D.3
D.3![]()
【答案】D
【解析】
根据题意,设M(x,y),求出![]() 点轨迹方程y2=4x,即可得M的轨迹是抛物线,其焦点为A(1,0),准线为x=﹣1,过点M作MD与准线垂直,且交准线于点D,分析可得直线x+(m﹣1)y+2m﹣5=0经过定点(3,﹣2),设P(3,-2),由点
点轨迹方程y2=4x,即可得M的轨迹是抛物线,其焦点为A(1,0),准线为x=﹣1,过点M作MD与准线垂直,且交准线于点D,分析可得直线x+(m﹣1)y+2m﹣5=0经过定点(3,﹣2),设P(3,-2),由点![]() 性质可得B在以AP为直径的圆上,由抛物线的定义可得又由|MA|=|MD|,则|MA|+|MB|=|MD|+|MB|,通过
性质可得B在以AP为直径的圆上,由抛物线的定义可得又由|MA|=|MD|,则|MA|+|MB|=|MD|+|MB|,通过![]() (
(![]() 为
为![]() 中点,圆心)结合图形分析可得答案.
中点,圆心)结合图形分析可得答案.
根据题意,设M(x,y),以MA为直径的圆的圆心为(![]() ,
,![]() ),
),
又由动点M满足以MA为直径的圆与y轴相切,则有(![]() )2=(
)2=(![]() 1)2+(
1)2+(![]() )2,
)2,
变形可得:y2=4x,
则M的轨迹是抛物线,其焦点为A(1,0),准线为x=﹣1,
过点M作MD与准线垂直,且交准线于点D,
设直线l为x+(m﹣1)y+2m﹣5=0,变形可得m(y+2)=y﹣x+5,
∴可得直线l经过定点(3,﹣2),
设P(3,-2),设AP的中点为C,则C的坐标为(2,﹣1),|CP|![]() ,
,
若AB⊥l,则B在以AP为直径的圆上,该圆的方程为![]() ,
,
又由|MA|=|MD|,则|MA|+|MB|=|MD|+|MB|,
则当C、M、D三点共线时,|MA|+|MB|取得最小值,且|MA|+|MB|取得最小值为圆![]() 上的点到D的最小值,
上的点到D的最小值,
此时|MA|+|MB|min=|CD|﹣r=3![]() ,
,
故选:D.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,上顶点坐标为
,上顶点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)问是否存在斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点,![]() ,
,![]() 的重心分别为
的重心分别为![]() ,且以线段
,且以线段![]() 直径的圆过原点,若存在,求出直线
直径的圆过原点,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,圆
,圆![]() (
(![]() 为坐标原点).过点
为坐标原点).过点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 交于点
交于点![]() ,与椭圆
,与椭圆![]() 的另一个交点的横坐标为
的另一个交点的横坐标为![]() .
.
(1)求椭圆![]() 的方程和圆
的方程和圆![]() 的方程;
的方程;
(2)过圆![]() 上的动点
上的动点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,若直线
,若直线![]() 的斜率为
的斜率为![]() 且
且![]() 与椭圆
与椭圆![]() 相切,试判断直线
相切,试判断直线![]() 与椭圆
与椭圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 的准线
的准线![]() 相切.
相切.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,若
,若![]() 的面积为6,求直线
的面积为6,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学家为研究对某病毒有效的疫苗,通过小鼠进行毒性和药效预实验.已知5只小鼠中有1只患有这种病毒引起的疾病,需要通过化验血液来确定患病的小鼠.血液化验结果呈阳性的即为患病小鼠,呈阴性即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病小鼠为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病小鼠为止;若结果呈阴性则在另外2只中任取1只化验.
(1)求方案甲化验次数X的分布列;
(2)判断哪一个方案的效率更高,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某校打算在长为1千米的主干道![]() 一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域
一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域![]() (
(![]() 为直角)和以
为直角)和以![]() 为直径的半圆形区域组成,点
为直径的半圆形区域组成,点![]() (异于
(异于![]() ,
,![]() )为半圆弧上一点,点
)为半圆弧上一点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,设
,设![]() ,且
,且![]() .初步设想把咨询台安排在线段
.初步设想把咨询台安排在线段![]() ,
,![]() 上,把宣传海报悬挂在弧
上,把宣传海报悬挂在弧![]() 和线段
和线段![]() 上.
上.
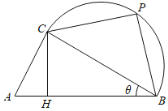
(1)若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让![]() 最大,求该最大值;
最大,求该最大值;
(2)若为了让学生了解更多的省外高校,贴出更多高校的海报,打算让弧![]() 和线段
和线段![]() 的长度之和最大,求此时的
的长度之和最大,求此时的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别是其左、右焦点,且过点
分别是其左、右焦点,且过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若在直线![]() 上任取一点
上任取一点![]() ,从点
,从点![]() 向
向![]() 的外接圆引一条切线,切点为
的外接圆引一条切线,切点为![]() .问是否存在点
.问是否存在点![]() ,恒有
,恒有![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线l的极坐标方程为ρcosθ=4,曲线C的极坐标方程为ρ=2cosθ+2sinθ,以极点为坐标原点O,极轴为x轴的正半轴建立直角坐标系,射线l':y=kx(x≥0,0<k<1)与曲线C交于O,M两点.
(Ⅰ)写出直线l的直角坐标方程以及曲线C的参数方程;
(Ⅱ)若射线l′与直线l交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com