
【题目】在直三棱柱![]() 中,
中,![]() 为正三角形,点
为正三角形,点![]() 在棱
在棱![]() 上,且
上,且![]() ,点
,点![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点.
的中点.
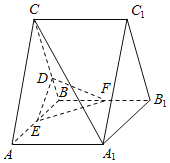
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接![]() ,连接
,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,再连接
,再连接![]() ,证明出
,证明出![]() ,结合条件
,结合条件![]() 可得出
可得出![]() ,然后利用直线与平面平行的判定定理可证明出
,然后利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明出
,证明出![]() 平面
平面![]() ,且
,且![]() ,设等边三角形
,设等边三角形![]() 的边长为
的边长为![]() ,并设
,并设![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,由
,由![]() 得出
得出![]() 的值,并计算出平面
的值,并计算出平面![]() 的法向量,利用空间向量法求出直线
的法向量,利用空间向量法求出直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
(1)如下图所示,连接![]() ,连接
,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,再连接
,再连接![]() ,
,
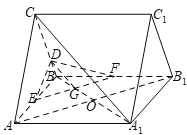
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,则
的中点,则![]() ,
,![]() ,则
,则![]() 为
为![]() 的中点,
的中点,
在直三棱柱![]() 中,
中,![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
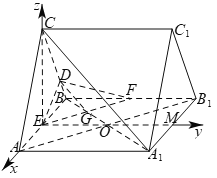
![]() 四边形
四边形![]() 为平行四边形,则
为平行四边形,则![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,所以,四边形
,所以,四边形![]() 是平行四边形,
是平行四边形,
![]() ,在直三棱柱
,在直三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 是等边三角形,且点
是等边三角形,且点![]() 是
是![]() 的中点,
的中点,![]() ,
,
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
设![]() 的边长为
的边长为![]() ,
,![]() ,则点
,则点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、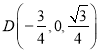 、
、![]() ,
,![]() ,
,![]() ,
,
![]() ,则
,则![]() ,得
,得![]() ,
,
![]() ,
,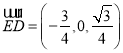 ,
,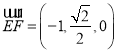 .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由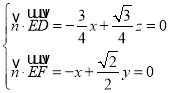 ,得
,得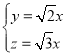 .
.
令![]() ,可得
,可得![]() ,
,![]() ,所以,平面
,所以,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
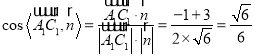 ,
,
因此,直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.
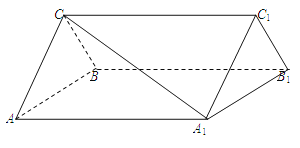
(Ⅰ)证明AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C 与平面BB1C1C所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上一动点,现将
上一动点,现将![]() 沿
沿![]() 折起,使点
折起,使点![]() 在面
在面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,当点
上,当点![]() 从
从![]() 运动到
运动到![]() ,则点
,则点![]() 所形成轨迹的长度为( )
所形成轨迹的长度为( )
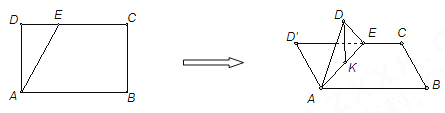
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.

(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的机器上有一种易损元件A,这种元件在使用过程中发生损坏时,需要送维修处维修.工厂规定当日损坏的元件A在次日早上 8:30 之前送到维修处,并要求维修人员当日必须完成所有损坏元件A的维修工作.每个工人独立维修A元件需要时间相同.维修处记录了某月从1日到20日每天维修元件A的个数,具体数据如下表:
日期 | 1 日 | 2 日 | 3 日 | 4 日 | 5 日 | 6 日 | 7 日 | 8 日 | 9 日 | 10 日 |
元件A个数 | 9 | 15 | 12 | 18 | 12 | 18 | 9 | 9 | 24 | 12 |
日期 | 11 日 | 12 日 | 13 日 | 14 日 | 15 日 | 16 日 | 17 日 | 18 日 | 19 日 | 20 日 |
元件A个数 | 12 | 24 | 15 | 15 | 15 | 12 | 15 | 15 | 15 | 24 |
从这20天中随机选取一天,随机变量X表示在维修处该天元件A的维修个数.
(Ⅰ)求X的分布列与数学期望;
(Ⅱ)若a,b![]() ,且b-a=6,求
,且b-a=6,求![]() 最大值;
最大值;
(Ⅲ)目前维修处有两名工人从事维修工作,为使每个维修工人每天维修元件A的个数的数学期望不超过4个,至少需要增加几名维修工人?(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选)已知函数![]() ,其中正确结论的是( )
,其中正确结论的是( )
A.当![]() 时,函数
时,函数![]() 有最大值.
有最大值.
B.对于任意的![]() ,函数
,函数![]() 一定存在最小值.
一定存在最小值.
C.对于任意的![]() ,函数
,函数![]() 是
是![]() 上的增函数.
上的增函数.
D.对于任意的![]() ,都有函数
,都有函数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,圆
,圆![]() :
:![]() 与
与![]() 轴的正半轴的交点是
轴的正半轴的交点是![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() .
.

(1)若直线![]() 与
与![]() 轴交于
轴交于![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的中点为
的中点为![]() ,点
,点![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com