
【题目】在如图所示的几何体中,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
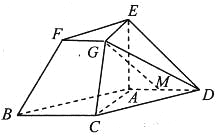
(1)若![]() 是线段
是线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题(1)连接![]() ,利用平行线的传递性结合
,利用平行线的传递性结合![]() 得到
得到![]() ,再利用点
,再利用点![]() 为
为![]() 的中点得到
的中点得到![]() ,从而证明四边形
,从而证明四边形![]() 为平行四边形,从而得到
为平行四边形,从而得到![]() ,最终结合直线与平面的判定定理证明
,最终结合直线与平面的判定定理证明![]() 平面
平面![]() ;(2)建立以点
;(2)建立以点![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的空间直角坐标系
轴的空间直角坐标系![]() ,利用空间向量法来求二面角
,利用空间向量法来求二面角![]() 的余弦值.
的余弦值.
试题解析:(1)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由于![]() ,因此
,因此![]() 连接
连接![]() ,由于
,由于![]() ,
,![]() ,
,
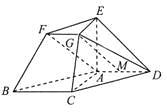
在平行四边形![]() 中,
中,![]() 是线段
是线段![]() 的中点,则
的中点,则![]() ,且
,且![]() ,
,
因此,![]() 且
且![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 、
、![]() 、
、![]() 两两垂直。
两两垂直。
分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,
,
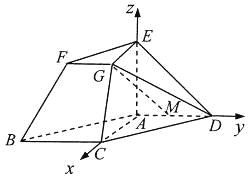
则![]() 、
、![]() 、
、![]() 、
、![]() ,
,
故![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
则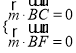 ,
,![]() ,取
,取![]() ,得
,得![]() ,所以
,所以![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则
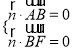 ,∴
,∴![]() ,取
,取![]() ,得
,得![]() ,所以
,所以![]() ,
,
所以![]()
故二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知F1,F2分别是双曲线C:![]() 的左、右焦点,若F2关于渐近线的对称点恰落在以F1为圆心,|OF1|为半径的圆上,则双曲线C的离心率为________.
的左、右焦点,若F2关于渐近线的对称点恰落在以F1为圆心,|OF1|为半径的圆上,则双曲线C的离心率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任利用周末时间对该班级![]() 年最后一次月考的语文作文分数进行统计,发现分数都位于
年最后一次月考的语文作文分数进行统计,发现分数都位于![]() 之间,现将所有分数情况分为
之间,现将所有分数情况分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共七组,其频率分布直方图如图所示,已知
共七组,其频率分布直方图如图所示,已知![]() .
.

(1)求频率分布直方图中![]() 、
、![]() 的值;
的值;
(2)求该班级这次月考语文作文分数的平均数和中位数.(每组数据用该组区间中点值作为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
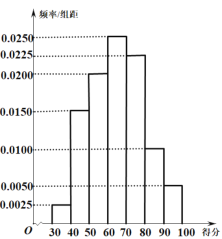
【题目】为了解广大学生家长对校园食品安全的认识,某市食品安全检测部门对该市家长进行了一次校园食品安全网络知识问卷调查,每一位学生家长仅有一次参加机会,现对有效问卷进行整理,并随机抽取出了200份答卷,统计这些答卷的得分(满分:100分)制出的频率分布直方图如图所示,由频率分布直方图可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
(1)请利用正态分布的知识求![]() ;
;
(2)该市食品安全检测部门为此次参加问卷调查的学生家长制定如下奖励方案:
①得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费:
的可以获赠1次随机话费:
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) |
|
|
概率 |
|
|
市食品安全检测部门预计参加此次活动的家长约5000人,请依据以上数据估计此次活动可能赠送出多少话费?
附:①![]() ;②若
;②若![]() ;则
;则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间.
的单调区间.
(2)设直线![]() 是曲线
是曲线![]() 的切线,若
的切线,若![]() 的斜率存在最小值-2,求
的斜率存在最小值-2,求![]() 的值,并求取得最小斜率时切线
的值,并求取得最小斜率时切线![]() 的方程.
的方程.
(3)已知![]() 分别在
分别在![]() ,
,![]() 处取得极值,求证:
处取得极值,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 。
。
(Ⅰ)如果存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,求满足上述条件的最大整数M;
(Ⅱ)如果对于任意的![]() 都有f(s)≥g(t)成立,求实数a的取值范围.
都有f(s)≥g(t)成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com