
分析 先设该农民种x亩水稻,y亩花生时,能获得利润z元,根据约束条件画出可行域,再利用几何意义求最值,目标函数表示直线在y轴上的截距的420倍,只需求出可行域直线在y轴上的截距最大值即可
解答 解:设该农民种x亩水稻,y亩花生时,能获得利润z元.
则z=(3×400-240)x+(5×100-80)y=960x+420y
即y=-$\frac{16}{7}$x+$\frac{z}{420}$…(2分)$\left\{\begin{array}{l}{x+y≤2}\\{240x+80y≤400}\\{x≥0,y≥0}\end{array}\right.$
即 $\left\{\begin{array}{l}{x+y≤2}\\{3x+y≤5}\\{x≥0,y≥0}\end{array}\right.$…(4分)
作出可行域如图阴影部分所示,…(8分)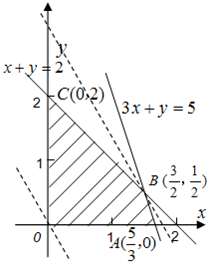
作出基准直线y=-$\frac{16}{7}$x,在可行域内平移直线y=-$\frac{16}{7}$x+$\frac{z}{420}$,
可知当直线过点B时,纵截距有最大值,…(10分)
由$\left\{\begin{array}{l}{x+y=2}\\{3x+y=5}\end{array}\right.$解得B($\frac{3}{2}$,$\frac{1}{2}$),…(12分)
故当x=1.5,y=0.5时,zmax=1650元,…(13分)
答:该农民种1.5亩水稻,0.5亩花生时,能获得最大利润,最大利润为1650元.
点评 本题主要考查了简单的线性规划在实际生活中的应用,以及利用几何意义求最值.在解决线性规划的问题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域②求出可行域各个角点的坐标③将坐标逐一代入目标函数④验证,求出最优解.


科目:高中数学 来源: 题型:填空题
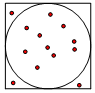 某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒500粒统计得到落在圆内的豆子数为390粒,则由此估计出的圆周率π的值为3.12.(精确到0.01)
某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒500粒统计得到落在圆内的豆子数为390粒,则由此估计出的圆周率π的值为3.12.(精确到0.01)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin20°<cos40°<tan50° | B. | cos40°<sin20°<tan50° | ||
| C. | tan50°<cos40°<sin20° | D. | sin20°<tan50°<cos40° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{6}$个长度单位 | ||
| C. | 向左平移$\frac{π}{12}$个长度单位 | D. | 向右平移$\frac{π}{12}$个长度单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC=2.
三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com