
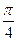 .
. 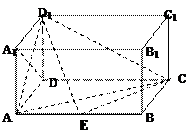
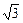 ,AA1 =
,AA1 =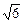 ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.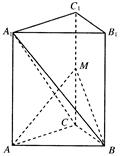
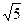 ,AD1=
,AD1= ,故
,故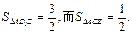
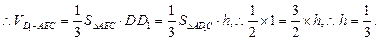

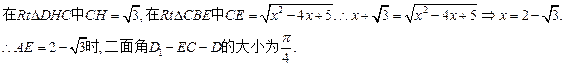
 (3)设平面D1EC的法向量
(3)设平面D1EC的法向量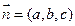 ,
,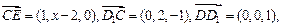
 令b="1," ∴c=2,a=2-x,∴
令b="1," ∴c=2,a=2-x,∴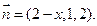 依题意
依题意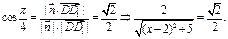 ∴
∴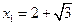 (不合,舍去),
(不合,舍去), ∴AE=
∴AE=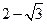 时,二面角D1—EC—D的大小为
时,二面角D1—EC—D的大小为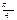 .
.  (Ⅲ)设点C到平面ABM的距离为h,易知BO =
(Ⅲ)设点C到平面ABM的距离为h,易知BO =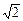 ,可知S△ABM =
,可知S△ABM = · AM · BO =
· AM · BO = ×
×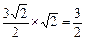 ∵VC – ABM = VM – ABC ∴
∵VC – ABM = VM – ABC ∴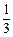 hS△ABM =
hS△ABM =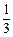 MC ·S△ABC
MC ·S△ABC 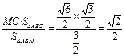 ∴点C到平面ABM的距离为
∴点C到平面ABM的距离为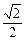 解法二:(Ⅰ)同解法一
解法二:(Ⅰ)同解法一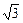 ,0,0),A1(
,0,0),A1(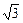 ,0,
,0,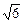 ),B (0,1,0),
),B (0,1,0),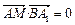 ,即– 3 + 0 +
,即– 3 + 0 +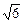 z1 = 0,故z1 =
z1 = 0,故z1 =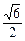 ,所以M (0,0,
,所以M (0,0,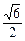 )
)  ,m⊥
,m⊥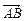 ,则
,则 即
即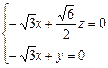 ,令x = 1,平面AMB的一个法向量为m = (1,
,令x = 1,平面AMB的一个法向量为m = (1,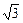 ,
,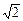 ),显然向量
),显然向量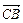 是平面AMC的一个法向量
是平面AMC的一个法向量 ,易知,m与
,易知,m与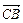 所夹的角等于二面角B—AM—C的大小,故所求二面角的大小为45°.(Ⅲ)所求距离为:
所夹的角等于二面角B—AM—C的大小,故所求二面角的大小为45°.(Ⅲ)所求距离为: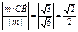 , 即点C到平面ABM的距离为
, 即点C到平面ABM的距离为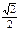


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
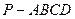 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 =2,
=2,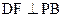 ,垂足为F。
,垂足为F。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
|
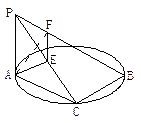
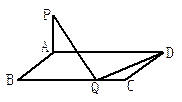
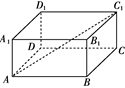 (第20题) (第21题)
(第20题) (第21题)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
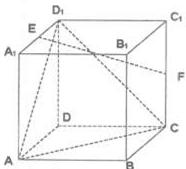
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 棱PA="PD" =
棱PA="PD" =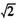 ,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.
,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.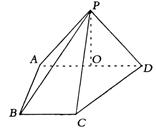
 PCD的距离.
PCD的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com