
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
下列有关命题的说法正确的是 ( )
A.“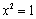 ”是“
”是“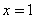 ”的充分不必要条件
”的充分不必要条件
B.“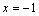 ”是“
”是“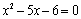 ”的必要不充分条件.
”的必要不充分条件.
C.命题“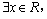 使得
使得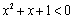 ”的否定是:“
”的否定是:“ 均有
均有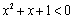 ”.
”.
D.命题“若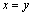 ,则
,则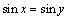 ”的逆否命题为真命题.
”的逆否命题为真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
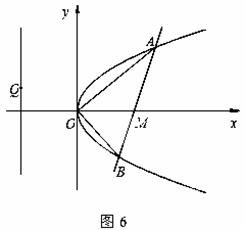
已知直线 过点
过点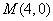 且与抛物线
且与抛物线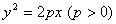 交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)设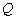 是直线
是直线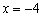 上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
某路段的雷达测速区检测点,对过往汽车的车速进行检测所得结果进行抽样分析,并绘制如图所示的时速(单位km/h)频率分布直方图,若在某一时间内有200辆汽车通过该检测点,请你根据直方图的数据估计在这200辆汽车中时速超过65km/h的约有( )

|
| A. | 30辆 | B. | 40辆 | C. | 60辆 | D. | 80辆 |
查看答案和解析>>
科目:高中数学 来源: 题型:
制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com