练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若f(x)＝－x2＋2ax与g(x)＝在区间[1,2]上都是减函数，则a的取值范围是(　　)

    A．(－1,0)∪(0,1)                                B．(－1,0)∪(0,1]

    C．(0,1)                                              D．(0,1]


    D　∵函数f(x)＝－x2＋2ax在区间[1,2]上是减函数，∴a≤1.

    又∵函数g(x)＝在区间[1,2]上也是减函数，∴a>0.∴a的取值范围是(0,1]．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在△ABC中，三边a、b、c成等比数列，角B所对的边为b，则cos2B+2cosB的最小值为（　　）

    A.                 B.-1                        C.                    D. 1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将a2＋b2＋2ab＝(a＋b)2改写成全称命题是(　　)

    A．∃a，b∈R，a2＋b2＋2ab＝(a＋b)2

    B．∃a<0，b>0，a2＋b2＋2ab＝(a＋b)2

    C．∀a>0，b>0，a2＋b2＋2ab＝(a＋b)2

    D．∀a，b∈R，a2＋b2＋2ab＝(a＋b)2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列函数中，不满足f(2x)＝2f(x)的是(　　)

    A．f(x)＝|x|                                         B．f(x)＝x－|x|

    C．f(x)＝x＋1                                     D．f(x)＝－x

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    具有性质：f＝－f(x)的函数，我们称为满足“倒负”变换的函数，下列函数：

    ①y＝x－；②y＝x＋；③y＝其中满足“倒负”变换的函数是(　　)

    A．①②　　                                       B．①③　　　C．②③　　　D．①

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)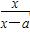＝(x≠a)．

    (1)若a＝－2，试证明f(x)在(－∞，－2)内单调递增；

    (2)若a>0且f(x)在(1，＋∞)内单调递减，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，一个几何体的正视图和侧视图是腰长为1的等腰三角形，俯视图是一个圆及其圆心，当这个几何体的体积最大时圆的半径是 （    ）

        A．       B．    C．    D．

     

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知.

       （1）若 ，函数在其定义域内是增函数，求的取值范围；

       （2）当，时，证明函数只有一个零点；

       （3）的图象与轴交于, ()两点，中点为，

            求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝x2 的值域是(　　)

    A．(0，＋∞)                                      B．(0,1)

    C．(0,1]                                              D．[1，＋∞)

    查看答案和解析>>

    同步练习册答案