
已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:
(1)过定点A(-3,4);
(2)斜率为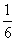 .
.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:
(1)对任意a∈R,a*0=a;
(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).
则函数f(x)=(ex)*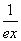 的最小值为( )
的最小值为( )
A.2 B.3
C.6 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
行四边形ABCD的一条对角线固定在A(3,-1),C(2,-3)两点,D点在直线3x-y+1=0上移动,则B点的轨迹方程为( )
A.3x-y-20=0 B.3x-y-10=0
C.3x-y-9=0 D.3x-y-12=0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l:kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线l不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com