
分析 (1)根据一元二次方程根的分布与系数的关系求出点(a,b)表示的区域,a2+b2表示点(a,b)到原点的距离的平方,求得它的范围.
(2)根据$\frac{|a+b-2|}{{\sqrt{2}}}$表示点(a,b)到直线a+b-2=0的距离,求得可行域内的点到直线a+b-2=0的距离的最大、最小值,可得$\frac{3}{{2\sqrt{2}}}<\frac{|a+b-2|}{{\sqrt{2}}}<\frac{3}{{\sqrt{2}}}$,
从而求得|a+b-2|的取值范围.
解答 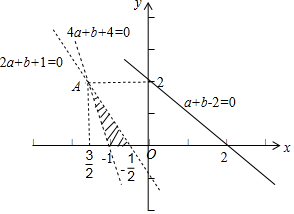 解:设f(x)=x2+2ax+b,则有$\left\{\begin{array}{l}f(0)>0\\ f(1)<0\\ f(2)>0\end{array}\right.?\left\{\begin{array}{l}b>0\\ 2a+b+1<0\\ 4a+b+4>0\end{array}\right.$,
解:设f(x)=x2+2ax+b,则有$\left\{\begin{array}{l}f(0)>0\\ f(1)<0\\ f(2)>0\end{array}\right.?\left\{\begin{array}{l}b>0\\ 2a+b+1<0\\ 4a+b+4>0\end{array}\right.$,
点(a,b)表示的区域为如图阴影部分,点A的坐标为(-$\frac{3}{2}$,2).
(1)a2+b2表示点(a,b)到原点的距离的平方,
∵$\frac{1}{2}<\sqrt{{a^2}+{b^2}}<\frac{5}{2}$,∴$\frac{1}{4}<{a^2}+{b^2}<\frac{25}{4}$.
(2)$\frac{|a+b-2|}{{\sqrt{2}}}$表示点(a,b)到直线a+b-2=0的距离,
点A到直线a+b-2=0的距离最小为$\frac{|-\frac{3}{2}+2-2|}{\sqrt{2}}$=$\frac{3}{2\sqrt{2}}$,
点(-1,0)到直线a+b-2=0的距离最大为$\frac{|-1+0-2|}{\sqrt{2}}$=$\frac{3}{\sqrt{2}}$,
故有 $\frac{3}{{2\sqrt{2}}}<\frac{|a+b-2|}{{\sqrt{2}}}<\frac{3}{{\sqrt{2}}}$,∴$\frac{3}{2}<|a+b-2|<3$.
点评 本题主要考查一元二次方程根的分布与系数的关系,简单的线性规划问题,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0” | |
| B. | 对命题p:?x∈R,使得x2+x+1<0,则?p:?x∈R,x2+x+1≥0 | |
| C. | 若x,y∈R,则“x=y”是“xy≥($\frac{x+y}{2}$)2中等号成立”的充要条件 | |
| D. | 已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α与平面β不垂直也不重合,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α⊥平面β,那么平面α内一定存在直线不垂直于平面β | |
| D. | 如果平面α⊥平面β,那么平面α内的所有直线都垂直于平面β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (A∪B)∪C=U | B. | (A∪B)∩C=∅ | C. | (A∩B)∩C=∅ | D. | (A∩B)∪C=C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com