
分析 对函数进行求导,通过导函数≤0,就是在(-∞,+∞)内单调递减,利用函数的最值,解之即可.
解答 解:函数g(x)=-x3+2x2+mx+5,g′(x)=-3x2+4x+m
∵函数g(x)=-x3+2x2+mx+5在(-∞,+∞)内单调递减,
∴g′(x)=-3x2+4x+m≤0在(-∞,+∞),恒成立,
即m≤3x2-4x,y=3x2-4x开口向上,对称轴是x=$\frac{2}{3}$,
函数3x2-4x≥3×$({\frac{2}{3})}^{2}$-4×$\frac{2}{3}$=$-\frac{4}{3}$.
∴m$≤-\frac{4}{3}$.
故答案为:(-∞,-$\frac{4}{3}$].
点评 本题主要考查函数的单调性与其导函数的正负之间的关系.即当导数大于0是原函数单调递增,当导数小于0时原函数单调递减.考查函数恒成立,转化思想的应用.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | -$\frac{3}{8}$ | C. | -$\frac{\sqrt{5}}{4}$ | D. | -$\frac{16}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| 指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 等级 | 一级优 | 二级良 | 三级轻度污染 | 四级中度污染 | 五级重度污染 | 六级严重污染 |
| A. | 6月份空气质量为优的天数为8天 | |
| B. | 6月份连续2天出现中度污染的概率为$\frac{2}{29}$ | |
| C. | 6月份北京空气质量指数AQI-PM2.5历史数据的众数为160 | |
| D. | 北京6月4至7日这4天的空气质量逐渐变好 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
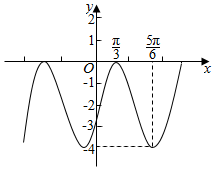 已知函数f(x)=sinωx(sinωx+2$\sqrt{3}$cosωx)+sin(ωx-$\frac{π}{4}$)sin(ωx+$\frac{π}{4}$)(其中ω为常数,且ω>0),函数g(x)=f(x)-$\frac{5}{2}$的部分图象如图所示.
已知函数f(x)=sinωx(sinωx+2$\sqrt{3}$cosωx)+sin(ωx-$\frac{π}{4}$)sin(ωx+$\frac{π}{4}$)(其中ω为常数,且ω>0),函数g(x)=f(x)-$\frac{5}{2}$的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com