
���� ��1�������оٷ�������⼴�ɣ�
��2�����ü��θ��������Ӧ�����������⼴�ɣ�
���  �⣺��1�����ҵ���ۿڵ�ʱ�������������1��1������1��2������1��3������3��1������3��2������3��3������5��1������5��2������5��3������9�֣�
�⣺��1�����ҵ���ۿڵ�ʱ�������������1��1������1��2������1��3������3��1������3��2������3��3������5��1������5��2������5��3������9�֣�
���мס�����ͬһ�쵽�øۿڵ��У�1��1������3��3������2�֣�
�ʼס�����ͬһ�쵽�øۿڵĸ���P=$\frac{2}{9}$��
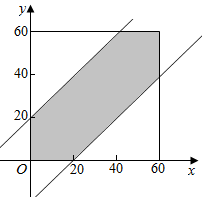
��2���ס��Ҿ�Ԥ����Ԫ��1��00��00��---01��00�������ʱ�̵���øۿڣ��������������ʱ��������20���ӣ���Ĵ�����Ҫ�ȴ���������x-y��20��y-x��20��
������������ʱ���ס������д�Ҫ�ȴ���Ϊ�¼�B��
��S��Ӱ=60��60-2��$\frac{1}{2}$��40��40=2000��S������=60��60=3600��
��P��B��=$\frac{2000}{3600}$=$\frac{5}{9}$��
���� ������Ҫ����ŵ���ͺͼ��θ��͵ĸ��ʼ��㣬�����оٷ��ǽ���ŵ���͵ij��÷���������ת�����ǽ�����θ��͵ij��÷�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1 | B�� | ��$\sqrt{2}$ | C�� | ��2 | D�� | ��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -2 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\frac{1}{2}$ | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24 | B�� | 8 | C�� | $\frac{8}{3}$ | D�� | $\frac{5}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com