
 AD,BE
AD,BE
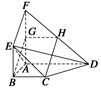
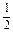 FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.

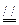
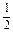 AD.
AD.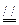
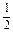 AD,故GH
AD,故GH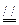 BC.
BC.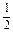 AF,G是FA的中点知,
AF,G是FA的中点知,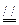 GF,所以EF∥BG.
GF,所以EF∥BG.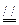 AG及∠BAG=90°知ABEG是正方形,故BG⊥EA.
AG及∠BAG=90°知ABEG是正方形,故BG⊥EA.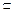 平面CDE,得平面ADE⊥平面CDE.
平面CDE,得平面ADE⊥平面CDE. =(0,b,0),
=(0,b,0), =(0,b,0),于是
=(0,b,0),于是 =
= .
. =(-a,0,c),
=(-a,0,c), =(-a,0,c),
=(-a,0,c),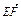 =
= .
. EF,H∈FD,故C、D、F、E四点共面.
EF,H∈FD,故C、D、F、E四点共面. =(-a,0,a),
=(-a,0,a), =(a,0,a).
=(a,0,a).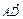 =(0,2b,0),因此
=(0,2b,0),因此 ·
· =0,
=0, ·
·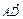 =0.
=0.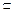 平面CDFE,得平面ADE⊥平面CDE.
平面CDFE,得平面ADE⊥平面CDE.

科目:高中数学 来源:不详 题型:单选题
| A.有两个面平行,其余各面都是四边形的几何体叫棱柱 |
| B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱 |
| C.一个棱柱至少有五个面、六个顶点、九条棱 |
| D.棱柱的侧棱长不都相等 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
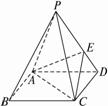
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
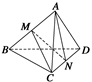
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
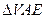 的面积是
的面积是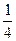 ,则侧棱VA与底面所成角的大小是__________________(结果用反三角函数值表示)。
,则侧棱VA与底面所成角的大小是__________________(结果用反三角函数值表示)。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 X∥Y”为真命题的是_________(填序号)
X∥Y”为真命题的是_________(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com