
分析 (1)化简可得m>x-x2对x>0恒成立,从而利用配方法化为最值问题即可;
(2)令f(x)=|x|+$\frac{m}{x}$-1=0化简可得m=$\left\{\begin{array}{l}{x-{x}^{2},x>0}\\{x+{x}^{2},x<0}\end{array}\right.$,从而转化为y=m和y=$\left\{\begin{array}{l}{x-{x}^{2},x>0}\\{x+{x}^{2},x<0}\end{array}\right.$的图象的交点个数,从而利用数形结合求解即可.
解答 解:(1)当x>0时,f(x)=x+$\frac{m}{x}$-1>0恒成立,
则有m>x-x2对x>0恒成立,
而x-x2=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$≤$\frac{1}{4}$,
故m>$\frac{1}{4}$;
(2)令f(x)=|x|+$\frac{m}{x}$-1=0得,
m=$\left\{\begin{array}{l}{x-{x}^{2},x>0}\\{x+{x}^{2},x<0}\end{array}\right.$,
函数f(x)的零点个数,
即y=m和y=$\left\{\begin{array}{l}{x-{x}^{2},x>0}\\{x+{x}^{2},x<0}\end{array}\right.$的交点个数,
在同一坐标系中作出函数的图象如下,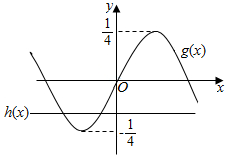
结合图象可知,
①m>$\frac{1}{4}$或m<-$\frac{1}{4}$时,有一个零点;
②m=±$\frac{1}{4}$或m=0时,有两个零点;
③-$\frac{1}{4}$<m<$\frac{1}{4}$且m≠0时,有三个零点.
点评 本题考查了函数的零点与函数的图象的交点的关系应用,同时考查了数形结合与分类讨论的思想应用.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:填空题
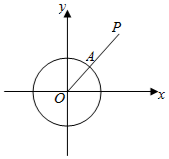 在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).
在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,f(x0)=0 | |
| B. | 若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 | |
| C. | 函数f(x)的图象是中心对称图形 | |
| D. | 若x0是f(x)的极值点,则f′(x0)=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,$\frac{π}{2}$),使得cosx>x | B. | ?x∈(0,$\frac{π}{2}$),使得cosx≥x | ||
| C. | ?x∈(0,$\frac{π}{2}$),使得cosx<x | D. | ?x∈(0,$\frac{π}{2}$),使得cosx<x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -4或0 | C. | 4或0 | D. | -4或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 240 | B. | 300 | C. | 360 | D. | 400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com