
| A. | ?x0∈R,f(x0)=0 | |
| B. | 若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 | |
| C. | 函数f(x)的图象是中心对称图形 | |
| D. | 若x0是f(x)的极值点,则f′(x0)=0 |
分析 求函数的导数,根据函数单调性,极值和导数的关系进行判断即可.
解答 解:A.当x→+∞时,f(x)→+∞,当x→-∞时,f(x)→-∞,即?x0∈R,f(x0)=0,故A正确,
B.(1)当△=4a2-12b>0时,f′(x)=0有两解,不妨设为x1<x2,列表如下
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
点评 本题考查命题的真假判断与应用,着重考查导函数与极值的应用,要求熟练掌握三次函数的图象和性质,属于中档题


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$<a<2$\sqrt{3}$ | B. | 2$\sqrt{2}$<a<$\frac{7}{2}$ | C. | 3<a<$\frac{7}{2}$ | D. | 3<a<2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
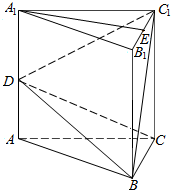 三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.
三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com