练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知正项等比数列{an}满足log2a1+log2a2+…+log2a2009=2009，则log2（a1+a2009）的最小值为2．

    分析 由对数的运算性质及可求a1•a2…a2009，结合等比数列的性质可求a1a2009，利用基本不等式即可求解

    解答 解：∵log2a1+log2a2+…+log2a2009=2009由对数的运算性质可得，log2a1•a2•••a2009=2009
    ∴a1•a2•••a2009=22009，
    由等比数列的性质可得，a1•a2009=a2•a2008=…=a10052，
    ∴a10052009=22009，
    ∵an＞0，
    ∴a1005=2，
    ∴a1•a2009=a2•a2008=…=a10052=4，
    由基本不等式可得，a1+a2009≥4，
    则log2（a1+a2019）≥2即最小值2，
    故答案为：2．

    点评 本题主要考查了对数的运算性质、等比数列的性质及利用基本不等是求解最值等知识的综合应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．已知ξ～B（n，0.3），Dξ=2.1，则n的值为（　　）
    A．10B．7C．3D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．（1）已知α为第二象限角，且 sinα=$\frac{\sqrt{15}}{4}$，求$\frac{sin（α+\frac{π}{4}）}{sin2α+cos2α+1}$的值．
    （2）已知α∈（0，$\frac{π}{4}$），β∈（0，π），且tan（α-β）=$\frac{1}{2}$，tanβ=-$\frac{1}{7}$，求tan（2α-β）的值及角2α-β．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．下面的程序运行后，输出的结果为4，1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设函数f （x）的导函数为f′（x），对任意x∈R都有f （x）＞f′（x）成立，则（　　）
    A．3f （ln2）＜2 f （ln3）B．3 f （ln2）=2 f （ln3）
    C．3 f（ln2）＞2 f （ln3）D．3 f （ln2）与2 f （ln3）的大小不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设$z=\frac{2}{1-i}+{（1-i）^2}$，则$|\overline z|$=（　　）
    A．$\sqrt{3}$B．1C．2D．$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知直线l：（m+2）x+（m-1）y+4-4m=0上总存在点M，使得过M点作的圆C：x2+y2+2x-4y+3=0的两条切线互相垂直，则实数m的取值范围是（　　）
    A．m≤1或m≥2B．2≤m≤8C．-2≤m≤10D．m≤-2或m≥8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．“五一”假期期间，某餐厅对选择A、B、C三种套餐的顾客进行优惠．对选择A、B套餐的顾客都优惠10元，对选择C套餐的顾客优惠20元．根据以往“五一”假期期间100名顾客对选择A、B、C三种套餐的情况得到下表：
    选择套餐种类ABC
    选择每种套餐的人数502525
    将频率视为概率．
    （I）若有甲、乙、丙三位顾客选择某种套餐，求三位顾客选择的套餐至少有两样不同的概率；
    （II）若用随机变量X表示两位顾客所得优惠金额的综合，求X的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．如图所示是一个三棱锥的三视图，则此三棱锥的外接球的体积为（　　）
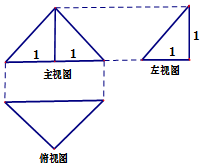
    A．$\frac{4}{3}π$B．$\frac{{\sqrt{3}}}{2}π$C．$\frac{{5\sqrt{5}}}{6}π$D．$\sqrt{6}π$

    查看答案和解析>>

    同步练习册答案