
| A. | 3f (ln2)<2 f (ln3) | B. | 3 f (ln2)=2 f (ln3) | ||
| C. | 3 f(ln2)>2 f (ln3) | D. | 3 f (ln2)与2 f (ln3)的大小不确定 |
分析 构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,利用导数可判断g(x)的单调性,由单调性可得g(ln2)与g(ln3)的大小关系,整理即可得到答案.
解答 解:令g(x)=$\frac{f(x)}{{e}^{x}}$,则g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$,
因为对任意x∈R都有f(x)>f′(x),
所以g′(x)<0,即g(x)在R上单调递减,
又ln2<ln3,所以g(ln2)>g(ln3),
即$\frac{f(ln2)}{{e}^{ln2}}$>$\frac{f(ln3)}{{e}^{ln3}}$,
即3f(ln2)>2f(ln3),
故选:C.
点评 本题考查导数的运算及利用导数研究函数的单调性,解决本题的关键是根据选项及已知条件合理构造函数,利用导数判断函数的单调性.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
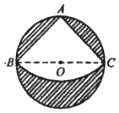 如图,有一直径为40cm的圆形铁皮,要从中剪出一个最大的圆心角为900的扇形铁皮ABC,把剪出的扇形围成一个圆锥,那么该圆锥的高为( )
如图,有一直径为40cm的圆形铁皮,要从中剪出一个最大的圆心角为900的扇形铁皮ABC,把剪出的扇形围成一个圆锥,那么该圆锥的高为( )| A. | $5\sqrt{2}cm$ | B. | 20cm | C. | $10\sqrt{7}cm$ | D. | $5\sqrt{30}cm$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{5}$ | B. | 3 | C. | 3或4 | D. | $\frac{6}{5}$或$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | T有最大值2 | B. | T有最小值1 | ||
| C. | T有最大值1 | D. | T没有最大值和最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{{({{a^x}+1})x}}{{{a^x}-1}}({a>0,a≠1})$ | B. | $y=\frac{{{a^x}-{a^{-x}}}}{2}({a>0,a≠1})$ | ||
| C. | $y=\left\{\begin{array}{l}1,({x>0})\\-1,({x<0})\end{array}\right.$ | D. | $y={log_a}\frac{1+x}{1-x}({a>0,a≠1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com