
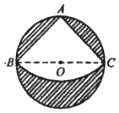
 如图,有一直径为40cm的圆形铁皮,要从中剪出一个最大的圆心角为900的扇形铁皮ABC,把剪出的扇形围成一个圆锥,那么该圆锥的高为( )
如图,有一直径为40cm的圆形铁皮,要从中剪出一个最大的圆心角为900的扇形铁皮ABC,把剪出的扇形围成一个圆锥,那么该圆锥的高为( )| A. | $5\sqrt{2}cm$ | B. | 20cm | C. | $10\sqrt{7}cm$ | D. | $5\sqrt{30}cm$ |
分析 由已知可得扇形周长,设出围成圆锥的底面半径,由圆锥底面圆的周长与展开图扇形弧长的关系求出已知底面半径,再由勾股定理求得圆锥的高.
解答 解:由已知图形可知,BC为圆的直径,则BC=40cm,
∴AB=$\frac{\sqrt{2}}{2}BC=20\sqrt{2}$cm,则$\widehat{BC}$=$\frac{π}{2}×20\sqrt{2}=10\sqrt{2}π$cm,
设围成圆锥的底面半径为r,则2πr=$10\sqrt{2}π$,得r=5$\sqrt{2}$cm,
而围成的圆锥的母线长为20$\sqrt{2}$,
∴高为$\sqrt{(20\sqrt{2})^{2}-(5\sqrt{2})^{2}}=5\sqrt{30}$.
∴圆锥的高为$5\sqrt{30}$cm.
故选:D.
点评 本题考查柱、锥、台体积的求法,考查圆锥底面圆的周长与展开图扇形弧长的关系,是中档题.


科目:高中数学 来源: 题型:填空题
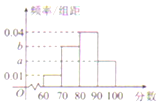 某校高三年级的一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取100人了解情况,已知70~80分数段抽取了30人,则全体高三年级学生的平均分数为82(以各组区间的中点值代表改组的取值)
某校高三年级的一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取100人了解情况,已知70~80分数段抽取了30人,则全体高三年级学生的平均分数为82(以各组区间的中点值代表改组的取值)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$e2 | B. | $\frac{{e}^{2}+1}{2}$ | C. | $\frac{{e}^{2}-1}{2}$ | D. | $\frac{{e}^{2}-3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 等腰梯形 | D. | 矩形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f (ln2)<2 f (ln3) | B. | 3 f (ln2)=2 f (ln3) | ||
| C. | 3 f(ln2)>2 f (ln3) | D. | 3 f (ln2)与2 f (ln3)的大小不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com