
| A�� | ƽ���ı��� | B�� | ���� | C�� | �������� | D�� | ���� |
���� �����������߶��������εĶ��弴���жϳ����ۣ�
��� �⣺��$\overrightarrow{AB}=3\overrightarrow e��\overrightarrow{CD}=-5\overrightarrow e��\overrightarrow e��\overrightarrow 0��$����$\overrightarrow{AB}$=-$\frac{3}{5}$$\overrightarrow{CD}$��
��$|{\overrightarrow{AD}}|=|{\overrightarrow{BC}}|$�����ı���ABCD�ǵ������Σ�
��ѡ��C��
���� ���⿼�����������߶��������εĶ��壬����������������������������ڻ����⣮


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
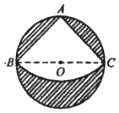 ��ͼ����һֱ��Ϊ40cm��Բ����Ƥ��Ҫ���м���һ������Բ�Ľ�Ϊ900��������ƤABC���Ѽ���������Χ��һ��Բ����ô��Բ�ĸ�Ϊ��������
��ͼ����һֱ��Ϊ40cm��Բ����Ƥ��Ҫ���м���һ������Բ�Ľ�Ϊ900��������ƤABC���Ѽ���������Χ��һ��Բ����ô��Բ�ĸ�Ϊ��������| A�� | $5\sqrt{2}cm$ | B�� | 20cm | C�� | $10\sqrt{7}cm$ | D�� | $5\sqrt{30}cm$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 120 | B�� | 26 | C�� | 20 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
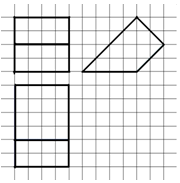 ��ͼ��������С�����εı߳�Ϊ$\frac{1}{2}$������������ij�ռ伸���������ͼ����ü���������Ϊ��������
��ͼ��������С�����εı߳�Ϊ$\frac{1}{2}$������������ij�ռ伸���������ͼ����ü���������Ϊ��������| A�� | 24 | B�� | 12 | C�� | 4 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | cosA | B�� | sinA | C�� | tanA | D�� | sin2A |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{6}{5}$ | B�� | 3 | C�� | 3��4 | D�� | $\frac{6}{5}$��$\frac{10}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=\frac{{��{{a^x}+1}��x}}{{{a^x}-1}}��{a��0��a��1}��$ | B�� | $y=\frac{{{a^x}-{a^{-x}}}}{2}��{a��0��a��1}��$ | ||
| C�� | $y=\left\{\begin{array}{l}1����{x��0}��\\-1����{x��0}��\end{array}\right.$ | D�� | $y={log_a}\frac{1+x}{1-x}��{a��0��a��1}��$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com