
分析 (1)由余弦定理得12a2+80a-347=0,由此能求出a.
(2)求出cosA=$\frac{\sqrt{6}}{3}$,从而sinA=$\frac{\sqrt{3}}{3}$,进而cos2A=cos2A-sin2A=$\frac{1}{3}$,再由余弦定理得cosB=$\frac{1}{3}$,由此得到cos2A=cosB,从而能求出λ.
解答 解:(1)∵△ABC中,角A,B,C的对边分别为a,b,c,c=$\frac{5}{2},b=\sqrt{6},4a-3\sqrt{6}$cosA=0.
∴4a=3$\sqrt{6}$×$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,
∵c=$\frac{5}{3}$,b=$\sqrt{6}$,∴12a2+80a-347=0,
解得a=$\frac{3}{2}$或a=-$\frac{49}{6}$(舍).
故a=$\frac{3}{2}$.
(2)由(1)可知cosA=$\frac{4}{3\sqrt{6}}$×$\frac{3}{2}$=$\frac{\sqrt{6}}{3}$,
∴sinA=$\frac{\sqrt{3}}{3}$,
∴cos2A=cos2A-sin2A=$\frac{1}{3}$,
∵$a=\frac{3}{2}$,c=$\frac{5}{2}$,b=$\sqrt{6}$,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{3}$,
∴cos2A=cosB,
∵△ABC中,c>b>a.∴B=2A,
∴λ=2.
点评 本题考查余弦定理、同角三角函数关系式、二倍角公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
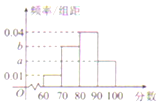 某校高三年级的一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取100人了解情况,已知70~80分数段抽取了30人,则全体高三年级学生的平均分数为82(以各组区间的中点值代表改组的取值)
某校高三年级的一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取100人了解情况,已知70~80分数段抽取了30人,则全体高三年级学生的平均分数为82(以各组区间的中点值代表改组的取值)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
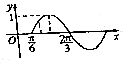 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{10}$,0) | B. | (0,10) | C. | (10,+∞) | D. | (1,10) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ | $\frac{7π}{3}$ | $\frac{17π}{6}$ |
| f(x) | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$e2 | B. | $\frac{{e}^{2}+1}{2}$ | C. | $\frac{{e}^{2}-1}{2}$ | D. | $\frac{{e}^{2}-3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 等腰梯形 | D. | 矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com