
分析 由$\frac{n}{a_n}=\frac{{2{a_{n-1}}+n-1}}{{{a_{n-1}}}}(n∈{N^*},n≥2)$,化为$\frac{n}{{a}_{n}}$-$\frac{n-1}{{a}_{n-1}}$=2,再利用等差数列的通项公式即可得出.
解答 解:∵$\frac{n}{a_n}=\frac{{2{a_{n-1}}+n-1}}{{{a_{n-1}}}}(n∈{N^*},n≥2)$,∴$\frac{n}{{a}_{n}}$-$\frac{n-1}{{a}_{n-1}}$=2,
则数列{$\frac{n}{{a}_{n}}$}为等差数列,公差为2,首项为3.
∴$\frac{n}{{a}_{n}}$=3+2(n-1)=2n+1.
∴an=$\frac{n}{2n+1}$.
故答案为:$\frac{n}{2n+1}$.
点评 本题考查了数列递推关系、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
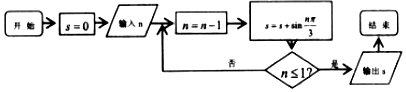
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com