
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
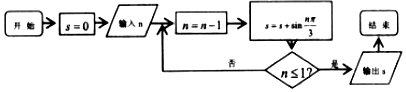
分析 执行程序框图,依次写出n,s的值,即可得出结论.
解答 解:执行程序框图,有
第一次循环后:n=9,s=0+0=0,
第二次循环后:n=8,s=$\frac{\sqrt{3}}{2}$;
第三次循环后:n=7,s=$\sqrt{3}$;
第四次循环后:n=6,s=$\sqrt{3}$;
第五次循环后:n=5,s=$\frac{\sqrt{3}}{2}$;
第六次循环后:n=4,s=0;
第七次循环后:n=3,s=0;
第八次循环后:n=2,s=$\frac{\sqrt{3}}{2}$;
第九次循环后:n=1,s=$\sqrt{3}$;退出循环,输出s的值为$\sqrt{3}$.
故选:A.
点评 本题主要考查程序框图和算法,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},2})$ | B. | $({\frac{1}{2},1})∪({1,2})$ | C. | (1,2) | D. | $({\frac{1}{2},∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 合情推理法 | B. | 综合法 | C. | 间接证法 | D. | 分析法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于命题p:?x∈R,x2+x+1>0,则¬p:?x∈R,x2+x+1≤0 | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | “sinθ=$\frac{1}{2}$”是“θ=30°”的充分不必要条件 | |
| D. | 命题“若x2-3x+2=0,则x=1”的逆否命题是“若x≠1,则x2-3x+2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f({x}_{0})-f({x}_{0}+△x)}{△x}$叫做函数y=f(x)在区间[x0,x0+△x](△x>0)的平均变化率 | |
| B. | 导数是一个常数 | |
| C. | 函数y=f(x)的导数f′(x)=$\underset{lim}{△x→0}$$\frac{f(x+△x)-f(x)}{△x}$ | |
| D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
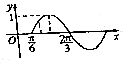 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com