
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用直线与平面平行的性质,判断①②③,
直线l作一平面γ,设γ∩α=a,γ∩β=b,过直线m作一平面π,设π∩α=c,π∩β=d,利用线面平行的性质定理和面面平行的判定定理即可判断出④.
解答 解:对于①,增加上l与m相交才能判断出α∥β,①错.
对于②③,α,β两个平面都有可能α与β相交,排除②和③.
对于④,过直线l作一平面γ,设γ∩α=a,γ∩β=b,∵l∥α,l∥β,则l∥a,l∥b,∴a∥β;
过直线m作一平面π,设π∩α=c,π∩β=d,∵m∥α,m∥β,则m∥c,m∥d,∴c∥β.
∵l与m是异面直线,∴a与c必定相交,∴α∥β.因此④正确.
故选:A.
点评 本题考查平面与平面平行的判定,考查直线与平面平行的性质,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{2})$ | B. | (1,2) | C. | $(\sqrt{2},\sqrt{3})$ | D. | $(\sqrt{3},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
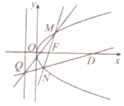 已知抛物线ω:y2=ax(a>0)上一点,P(t,2)到焦点F的距离为2t
已知抛物线ω:y2=ax(a>0)上一点,P(t,2)到焦点F的距离为2t查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(2,+∞) | C. | (-∞,-2)∪(-2,0) | D. | (0,2)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com